- Introduction
- Asymptotic Computational Complexity
- Asymptote
- Asymptotic Analysis
- Big O
- Big Omega
- Big Theta
- The Differences Between These Three
- The Worst, Best, Average/Expected Case Context
- References
- Translations
Before we head into the website, we need to know what is Asymptotic Computational Complexity first. If you were already familiar with this term, just skip and jump into the Big-O Cheat Sheet Website.
In computational complexity theory, asymptotic computational complexity is the usage of asymptotic analysis for the estimation of computational complexity of algorithms and computational problems, commonly associated with the usage of the big O notation. - Wikipedia
To understand those terms, we need to know what is an Asymptote first before we deep dive into Asymptotic Analysis.
In analytic geometry, an asymptote of a curve is a line such that the distance between the curve and the line approaches zero as one or both of the x or y coordinates tends to infinity. - Wikipedia
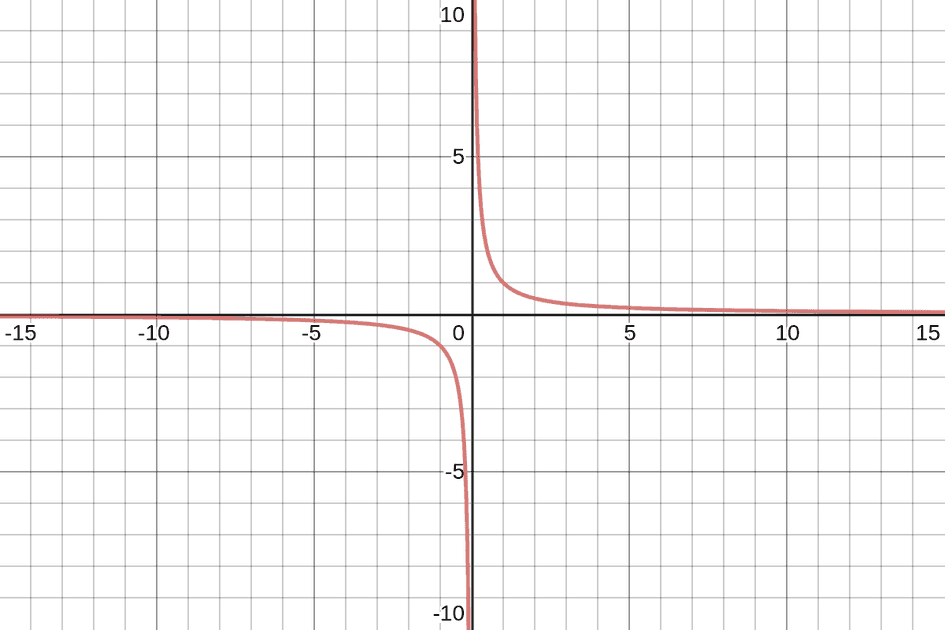
Here's a visual example from jarednielsen
y = 1/x
No matter how large (or small) the value of x, our curve will never touch the x or y axes. Even if that number is Infinity. 🐢🏃♀️. Especially if that number is zero. Why? It’s mathematically impossible to divide by 0. In the chart above, the x and y axes are the asymptotes of the equation
y = 1 / x. But any line can be an asymptote. We’re not limited to horizontal and vertical lines. - jarednielsen
Now we get the idea of an asymptote, let's continue to learn about Asymptotic Analysis.
In mathematical analysis, asymptotic analysis, also known as asymptotics, is a method of describing limiting behavior. - Wikipedia
For example, we get from jarednielsen.
Given this function f(x) = x^2 + 2x , x increases in value (approaches infinity) and 2x becomes insignificant compared to x^2. We then simply say that f(x) is asymptotically equivalent to x^2
Why do we need this asymptotic analysis you might ask?
Because we need to estimate the computational complexity of algorithms and computational problems. To get everyone on the same page, we use these notations: big O, big Ω and big θ to describe a different type of estimation.
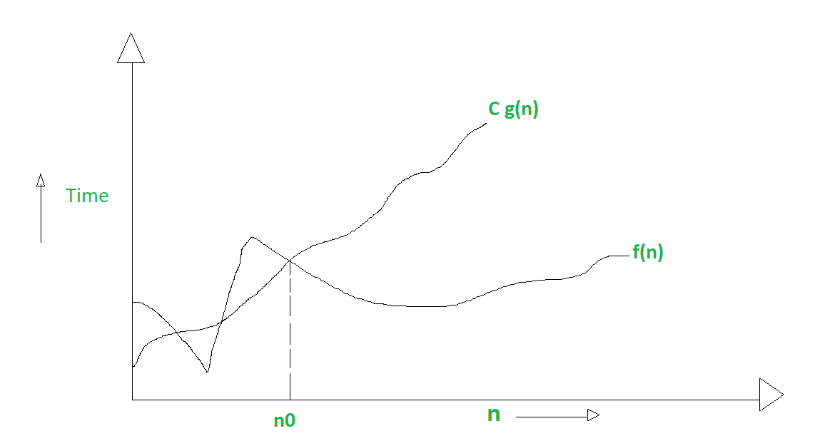
Big O describes the upper bound of an algorithm. This is why, for us, as developers and practitioners, we are primarily concerned with Big O. We want to know just how poorly an algorithm might perform. - jarednielsen
It is define as upper bound and upper bound on an algorithm is the most amount of time required (the worst case performance). Big O notation is used to describe asymptotic upper bound. - GeeksForGeeks
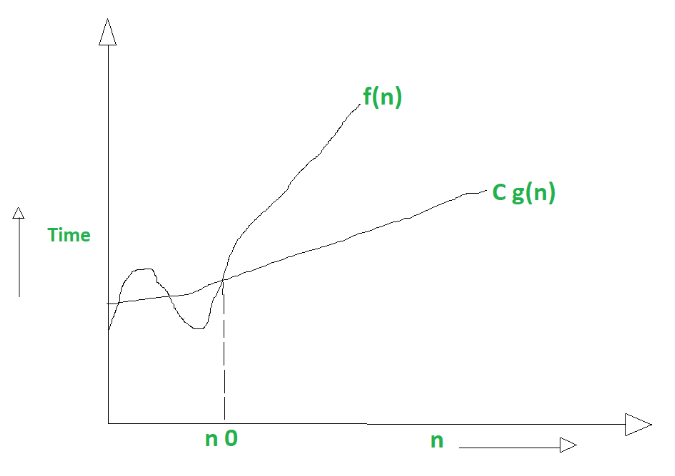
Big Omega describes the lower bound of an algorithm. If only life always handed us sorted arrays. 🌼. We can also think of this as our best-case scenario. - jarednielsen
It is define as lower bound and lower bound on an algorithm is the least amount of time required (the most efficient way possible, in other words best case). Just like O notation provide an asymptotic upper bound, Ω notation provides asymptotic lower bound. - GeeksForGeeks
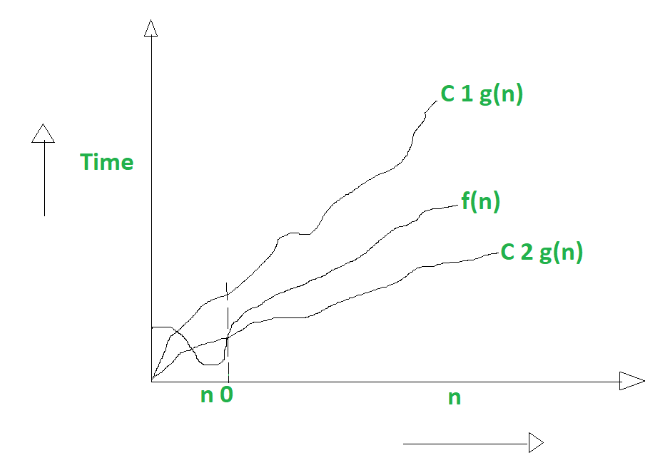
Big Theta describes the tight bound of an algorithm, it’s limit from above and below. Big Theta is often used to describe the average, or expected, case for an algorithm. This isn’t exactly true, but it’s a useful shorthand. - jarednielsen
It is define as tightest bound and tightest bound is the best of all the worst case times that the algorithm can take. - GeeksForGeeks
| Big O | Big Ω / Omega | Big θ / Theta | |
|---|---|---|---|
| Conditional operator-wise | <= |
>= |
== |
| Rate of growth of an algorithm / data structure | is less than | is greater than | is equal to |
| Bound | upper | lower | above and below |
| Notation | O(n) |
Ω(n) |
θ(n) |
What is the relationship between
best case / worst case / expected case
and
Big O / Big Omega (Ω) / Big Theta (θ)?
There isn’t one.
Equivalencies are often made between Big O and worst case, Big Omega and best case, and Big Theta and average case, but we can speak of best, worst, and average for each of these notations. - jarednielsen
For example, each of the following statements about worst case are true:
Insertion Sort’s worst case rate of growth is at most
O(n^2)
Insertion Sort’s worst case rate of growth is at leastΩ(n)
Insertion Sort’s worst case rate of growth is exactlyΘ(n^2)
Big-O Cheat Sheet Website ◽ last accessed 6 September 2022
Asymptotic computational complexity ◽ last accessed 6 September 2022
Asymptote ◽ last accessed 6 September 2022
Asymptotic analysis ◽ last accessed 6 September 2022
What’s the Difference Between Big O, Big Omega, and Big Theta? ◽ last accessed 6 September 2022
Difference between Big Oh, Big Omega and Big Theta ◽ last accessed 6 September 2022
- 🇮🇩 Indonesian: