docs: 이진탐색

docs/.vuepress/config.js

@@ -34,6 +34,10 @@ module.exports = {
         title: 'Front End',
         children: CONST.FrontEndList,
       },
+      {
+        title: 'Alogorithm',
+        children: CONST.Alogorithm,
+      },
       {
         title: 'VuePress',
         children: CONST.VuePressList,

docs/.vuepress/const.js

@@ -27,6 +27,7 @@ exports.JavaScriptList = [
 exports.VuejsList = ['Vue/hellovue.md', 'Vue/vue-sheetjs.md']
 exports.FastApiList = ['fastapi/crawl.md', 'fastapi/db.md']
 exports.FrontEndList = ['frontend/bem.md', 'frontend/npm.md']
+exports.Alogorithm = ['Alogorithm/binary_search.md']
 exports.VuePressList = [
   'vuepress/vuepress-start.md',
   'vuepress/vuepress-deploy.md',

docs/Alogorithm/binary_search.md

@@ -0,0 +1,104 @@
+# 이분 탐색
+
+- 이진 탐색은 정렬돼 있는 데이터에서 특정한 값을 찾아내는 알고리즘이다.
+- 시간복잡도 logn
+- 장점
+  - 검색 속도가 빠르다. (추가적인 메모리를 사용하지 않음)
+  - 검색 대상이 매우 큰 경우에도 탐색 시간이 빠르기 때문에, 대량의 데이터를 다루는 알고리즘에서 많이 사용된다.
+- 단점
+  - 반드시 특정구조가 필요하다. (배열이나 이진탐색 트리와 같이 정렬된 구조에서만 사용가능)
+
+## 배열에서 동작방식
+
+key 값 39를 찾아보자.
+
+값을 선형으로 탐색하면 n이 걸리겠지만 이분탐색을 사용하여 검색하게 된다면 logn의 시간이 나온다.
+
+1. 배열의 중간 값을 가져온다. (low = 0, high = 9, mid =4)
+
+```python
+mid  = low + (high - low) / 2
+          = 0 + (9-0)/2
+          = 4
+```
+
+![alt text](https://img1.daumcdn.net/thumb/R1280x0/?scode=mtistory2&fname=https%3A%2F%2Fblog.kakaocdn.net%2Fdn%2F8giC7%2FbtrW9mzhunB%2F5MGJL2tHabyDc2MeoEKvmk%2Fimg.png)
+
+- 중앙값과 검색 값을 비교합니다.
+- A [4] (27) < key (39) 이므로 배열의 오른쪽 구간을 검색 범위로 정한다.
+
+2. 배열의 중간 값을 가져온다. (low = 5, high = 9, mid = 7)
+
+```python
+mid  = low + (high - low) / 2
+          = 5 + (9-5)/2
+          = 7
+```
+
+![alt text](https://img1.daumcdn.net/thumb/R1280x0/?scode=mtistory2&fname=https%3A%2F%2Fblog.kakaocdn.net%2Fdn%2FsvMMj%2FbtrXaCaw38f%2FsuadNfLM5KbQFDKgGQAx40%2Fimg.png)
+
+- 중앙 값과 검색 값을 비교합니다.
+- A [7] (45) > key (39) 이므로 배열의 왼쪽 구간을 탐색 범위로 정한다.
+
+3. 중앙 값을 결정 (low = 5, high = 6, mid = 5)
+   ![alt text](<[image-3.png](https://img1.daumcdn.net/thumb/R1280x0/?scode=mtistory2&fname=https%3A%2F%2Fblog.kakaocdn.net%2Fdn%2FcXVWDh%2FbtrXameGoA9%2FMhIe2FviwLTx6ANlNJDkIk%2Fimg.png)>)
+
+```python
+mid  = low + (high - low) / 2
+        = 5 + (6-5)/2
+        = 5
+```
+
+- 중앙값과 검색 값을 비교합니다.
+- A [5] (32) < key (39) 이므로 배열의 오른쪽 구간을 탐색 범위로 정한다.
+- 그러고 나면 배열의 요소는 1개만 남았으므로 39가 되고 우리가 찾으려는 값과 일치하게 된다.
+  ![alt text](https://img1.daumcdn.net/thumb/R1280x0/?scode=mtistory2&fname=https%3A%2F%2Fblog.kakaocdn.net%2Fdn%2FnsRkN%2FbtrW9lHapD1%2FpZuR9w1ZkwV25RG7FWbGv0%2Fimg.png)
+
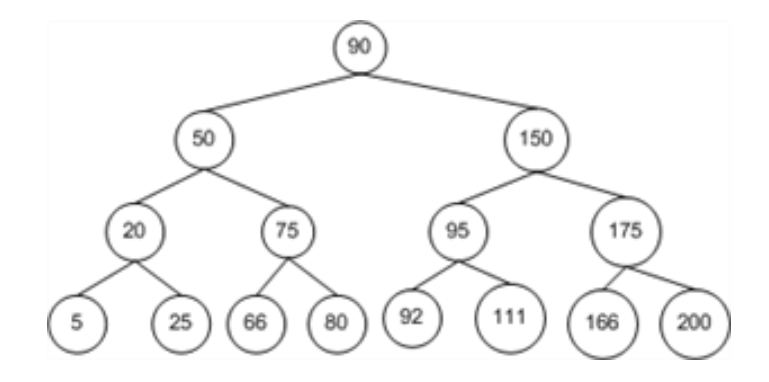
+## 트리에서 동작방식
+
+![alt text](https://velog.velcdn.com/images/kwontae1313/post/7b57aa6b-6925-4746-a134-501812a44db1/image.png)
+
+- 트리에서 중간 노드를 찾는다.
+- 찾으려는 값과 중간 노드의 값과를 비교한다.
+- 찾으려는 값이 중간 노드의 값보다 작으면 왼쪽 하위 트리에서 탐색을 계속한다.
+- 찾으려는 값이 중간 노드의 값보다 크면 오른쪽 하위 트리에서 탐색을 계속한다.
+- 탐색 범위를 반으로 좁힌다.
+- 탐색 범위가 더 이상 없을 때까지 위 과정을 반복한다.
+
+## 시간복잡도 logn 공식 유도
+
+- 배열의 길이를 (n)이라고 할 때, 처음 탐색 범위는 전체 배열, 즉 (n)개의 요소입니다.
+- 첫 번째 단계에서 중간값을 확인한 후, 탐색 범위를 반으로 줄여 (n/2)개의 요소만을 대상으로 합니다.
+- 두 번째 단계에서 다시 탐색 범위를 반으로 줄여 (n/4)개의 요소를 대상으로 합니다.
+- 이 과정을 (k)번 반복하면, 탐색 범위는 (n/2^k)개의 요소가 됩니다.
+- 시간 복잡도 유도를 수식으로 표현하면
+- [n/2^k = 1]
+- [2^k = n]
+- [log_2(2^k) = log_2(n)]
+- [k = log_2(n)]
+
+## 코드
+
+```python
+def binary_search(arr, find_num):
+  L=0
+  R=len(arr)-1
+
+  while L<=R: # 탈출 조건: L이 R보다 커지면 탐색할 숫자가 없는 경우임
+
+    pivot = (L+R)//2  # 탐색 범위를 반으로 나눔
+
+     # 찾는 숫자가 pivot보다 클경우 pivot의 위츠를 +1 한 위치로 이동
+    if arr[pivot] < find_num:
+      L=pivot+1
+     # 찾는 숫자가 pivot보다 작을경우 pivot의 위츠를 -1 한 위치로 이동
+    elif arr[pivot] > find_num:
+      R=pivot-1
+    else: # 탐색 성공
+      return True
+  return False
+
+arr = [-3,5,15,24,27,32,29,49,53,61]
+num = 49 # 검색할 숫자
+binary_search(arr, num):
+```