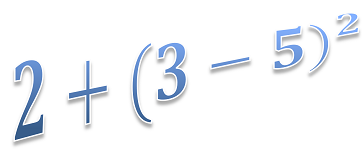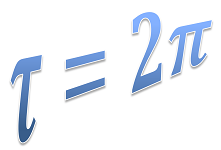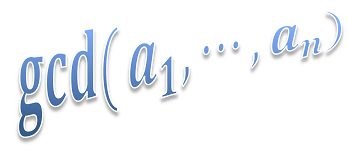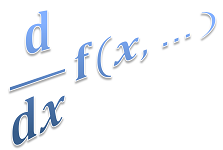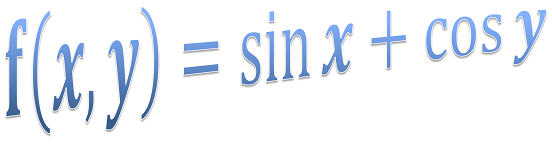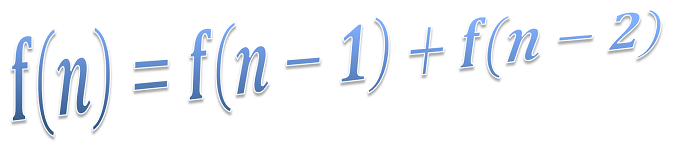mXparser - a super easy, rich and highly flexible Mathematical Expression Parser (Math Parser, Expression Evaluator) library for JAVA, Kotlin, Android, C++, C# .NET
v.6.0.0 (2024-05-19): Translations (French, German, Italian, Polish, Portuguese, Spanish) + New operators
- mXparser in French,
- mXparser in German,
- mXparser in Italian,
- mXparser in Polish,
- mXparser in Portuguese,
- mXparser in Spanish,
- #303 #304 #305 #306 #307 #308
v.5.2.1 (2023-02-08): Orion: Improvement and standardization of descriptions and messages. Definition of your own translations. Exporting help in multiple formats. Clones for thread safe. Performance improvement.
- Improvement and standardization of built-in elements description, click to see usage example
- Improvement and standardization of error messages, click to see usage example
- Definition of your own translations, click to see usage example
- Help content in the CSV format, click to see usage example
- Help content in the HTML format, click to see usage example
- Help content in the Markdown format, click to see usage example
- Help content in the JSON format, click to see usage example
- Clones for thread safe, click to see usage example
- Performance improvement for calculations in the loop, click to see usage example
- Bug fixed #291 Euler polynomial function producing wrong results
- Bug fixed #292 Implied Multiplication bug when blank character separates
- Bug fixed #283 Unnecessary newline at the end in getErrorMessage()
- Bug fixed #284 Unnecessary space in function expression string returned by getErrorMessage()
- Bug fixed #297 Claculation Steps Register fix - commas / parenthesis / missing parts related to user arguments
v.5.1 Libris: Implied Multiplication, Unicode Math Symbols, Additional Probability Distributions, Calculation Steps Register, Serialization Support
- Implied Multiplication, click to see usage example
- Unicode Math Symbols, click to see usage example
- Calculation Steps Register, click to see usage example
- Serialization Support, click to see usage example
- An Attempt To Fix Expression String
- Student's t-distribution: Probabilisty Density Function, Cumulative Distribution Function, Quantile Function
- Chi-Squared Distribution: Probabilisty Density Function, Cumulative Distribution Function, Quantile Function
- F-Snedecor Distribution: Probabilisty Density Function, Cumulative Distribution Function, Quantile Function
- Minor Bug fixing: 259, 258, 252, 261, 262, 263, 271, 269, 268, 266, 265
- Regression tests refactoring
Install-Package MathParser.org-mXparser -Version 6.1.0
dotnet add package MathParser.org-mXparser --version 6.1.0
<PackageReference Include="MathParser.org-mXparser" Version="6.1.0"/>
<dependency>
<groupId>org.mariuszgromada.math</groupId>
<artifactId>MathParser.org-mXparser</artifactId>
<version>6.1.0</version>
</dependency>
implementation 'org.mariuszgromada.math:MathParser.org-mXparser:6.1.0'
implementation("org.mariuszgromada.math:MathParser.org-mXparser:6.1.0")
include(FetchContent)
FetchContent_Declare(
MathParserOrgMxParser
GIT_REPOSITORY https://github.com/mariuszgromada/MathParser.org-mXparser.git
GIT_TAG v.6.1.0
SOURCE_SUBDIR CURRENT/cpp/lib
)
FetchContent_MakeAvailable(MathParserOrgMxParser)
target_link_libraries(YourExecutable MathParserOrgMxParser)
$ npm i mathparser.org-mxparser
- or consider donation: DONATION
mXparser is a highly flexible parser of mathematical expressions provided as text. Software delivers easy to use API for JAVA, C# .NET, TypeScript and JavaScript.
- JAVA: 6+
- Android - tested with mxparser compiled using jdk 1.7
- .NET Framework (2+) / MONO CLS, .NET Core: 1+, .NET Standard: 1+, .NET PCL
- Xamarin
- TypeScript, JavaScript
- Chrome, Firefox, MS Edge, Safari
- nodeJS
The tutorial consists of c.a. 180 live examples from c.a. 40 sections. Each of the examples can be copied and run on your own environment. In addition, mXparser provides an extensive collection of over 500 built-in math functions, expressions and symbols. Familiarize yourself with the scope and the syntax. Live testing is the best way to learn. Good luck!
- Full help content
- In-line help searching
- Simple calculation
- Changing expression string
- Using operators
- Power function
- Using numbers in scientific notation
- Percent sign
- Leading zeros
- Numbers and parenthesis
- Numbers and constants / arguments
- Numbers and constants / arguments and parenthesis
- Numbers and constants / arguments and parenthesis and functions
- Implied multiplication and possible ambiguity
- Implied multiplication and list of tokens
- Enable / disable implied multiplication
- Binary relation “=”
- Binary relation “<“
- Boolean operator “OR”
- Boolean operator “AND”
- Unary function
- Binary function
- Function with 3 arguments
- Function with n-arguments
- Function with even number of arguments
- Defining constant – various options
- Dealing with free arguments
- Defining dependent arguments
- Implementing your own Argument Extension
- Getting list of missing user defined arguments
- Possible conflict between Implied Multiplication and getting list of missing user defined arguments + recommended solutions
- Fast function definition (performance of creation)
- Handy function constructor, but slower proces of function creation (performance of creation slower, but calculation the same)
- Function with more parameters
- Function in function
- Implementing your own Function Extension
- Getting list of missing user defined functions
- Possible conflict between Implied Multiplication and getting list of missing user defined functions + recommended solutions
- What is pre-compilation?
- When is pre-compilation done?
- When is pre-compilation done again?
- An example of bad practice in computing the value of an expression for a changing argument value
- An example of good practice in computing the value of an expression for a changing argument value
- Function returning number of parameters provided
- Function returning sum of first and last parameter provided
- Function returning parameter at position defined by the first parameter
- Function returning sum of all parameters squared
- Implementing your own Variadic Function Extension
- Mechanics of the if function
- “if” function and arguments
- “if” function in user defined function
- Mechanics of the “iff” function
- iff function is not limited in number of cases
- SIGMA summation operator
- PI product operator
- SIGMA summation operator – Approximating sin(x) by Taylor series
- SIGMA summation operator – Approximating pi value by integrating sqrt(1-x^2)
- General derivative
- Left / right derivative
- Derivative from more complex function
- Derivative – alternative syntax
- Integrals – calculating pi by integration sqrt(1-x^2)
- Solve 2x-4 = 0 for x in [0, 10]
- Solve cos(x) = 0 for x in [0, pi]
- Solve cos(x) = 0 for x in [pi, pi] (root not bracketed)
- Solve x-y = 0 for x in [0, 10] and y = 4
- Solve sin'(x) = 0 for x in [0, pi]
- Primality test function
- Primes counting function
- Using built-in primes cache to accelerate calculations
- Estimating number of primes using Offset logarithmic integral function
- Prime factorization
- Using built-in constants
- Estimating Moon gravitational acceleration
- Getting list of constants
- Units of length / distance
- Units of time
- Units of information
- Units of volume
- Express 4 feet in inches
- Express in square kilometers the area of a rectangle measuring 100 meters by 2 kilometers
- List of supported units
- Example: 10 Millions / Kilo
- List of supported metric prefixes
- Expected value estimation using Probability Distribution Function
- Probability estimation using Cumulative Distribution Function – the law of 3*SIGMA
- Calculating quantiles using Inverse Cumulative Distribution Function – males height example assuming males height distribution N(170, 15)
- Random number from uniform continuous distribution
- Random number from uniform discrete distribution
- Random number from normal distribution
- Random number from a given list
- Estimating mean of Normal distribution
- Estimating standard deviation of Normal distribution
- Estimating variance of Normal distribution
- Random integer
- Random integer N: -10^k <= N <= 10^k for k = 1, 2, …,9
- Random natural number
- Random natural number N <= 10^k for k = 1, 2, …,9
- Uniform continuous distribution U(0,1)
- Normal distribution N(0,1)
- Dependent argument as user defined random variable
- User defined function as user defined random variable – random walk example
- Bitwise unary complement
- Bitwise AND
- Bitwise exclusive OR
- Bitwise inclusive OR
- Signed left / right shift
- Fraction (proper) as Number Literal
- Improper Fraction as Number Literal
- Fraction (Mixed Number) as Number Literal
- Fraction (Mixed Numer) and Improper Fraction in one Number Literal
- Operations on Fractions
- Represent double as Fraction
- Binary number
- Octal number
- Hexadecimal number
- Unary number
- Unary zero
- Base 1 – 36 number literals
- Base N numeral system
- Fibonacci numbers using fast recursion
- Fibonacci numbers using user defined recursive function
- Number of recursive parameters is not limited – binomial coefficient definition using user defined recursive function
- Mixing function parameters – part causing recursive calls, other part as ‘typical’ parameter. Below example is presenting definition of Chebyshev polynomial using recursive function.
- Indirect recursion – approximating sin(x) and cos(x)
- The square root √
- The square root of the square root √√
- The square root and parenthesis √()
- The roots of various orders ∜ ∛ √
- SIGMA summation operator ∑
- Unicode name of a user defined argument
- Show all Unicode built-in keywords
- Enable / disable Unicode built-in keywords
- List of Unicode symbols that grammar accepts
- NaN in condition
- NaN symbol
- First non-NaN value
- Basic trigonometric function
- Inverse trigonometric function
- Using units of angle being in radians mode
- Simple Expression
- Dependent User Argument
- User Function
- Expression referencing User Argument and User Function
- Setting the verbose mode
- Syntax checking
- Lexical syntax checking
- Getting computing time
- Printing expression tokens
- Using tokens to print expression in a fancy way
- Playing with invalid tokens
- Removing built-in tokens
- Modifying built-in tokens
- Overriding built-in tokens
- A few words on Floating Point Math
- Why mXparser is based on the double data type?
- Smart rounding options available in mXparser
- Check which rounding settings are currently active
- Example - Only Canonical Rounding option is active
- Example - Only Unit In The Last Place Rounding option is active
- Example - Only Almost Integer Rounding option is active
- Example - None of the rounding options are active
- User expression in the loop + output
- User function in the loop + output
- User argument (dependent) in the loop + output
- User expression in the loop – Performance
- User function in the loop – Performance
- User argument (dependent) in the loop – Performance
- Degrees / Radians Mode
- Attempt To Fix Expression String Mode
- Primes Cache
- Epsilon Comparison / Exact Comparison Mode
- Canonical Rounding Mode
- ULP (Unit In The Last Place) Rounding Mode
- Almost Integers Rounding Mode
- Implied Multiplication Mode
- Unicode Builtin Key Words Mode
- Verbose / Silent Mode
- Override Builtin Tokens Mode
- Modify Builtin Tokens Mode
- Remove Builtin Tokens Mode
- Current Calculation Cancellation
- Setting Console Prefix
- Reaching Console Output String
- Maximum Allowed Recursion Depth
- Double to Fraction Conversion
- Random Generator Selection
- Maximum Threads Number
- Default Settings
- SerializationUtils class
- Binary serialization SECURITY WARNING
- Enabling / Disabling binary serialization
- Expression serialization / deserialization from / to byte[]
- Expression serialization / deserialization from / to String
- Expression serialization / deserialization from / to File
- Serialization / Deserialization of complex objects
mXparser provides a rich collection of built-in math functions, math expressions, and math symbols. Familiarize yourself with the scope and the syntax. Math collection internal help is also available directly from the software – see the tutorial and the API documentation for all the details.
- Units
- basic operators, i.e.: +, -, *, ^, !
- Boolean logic operators i.e.: or, and, xor
- binary relations i.e.: =, <, >
- math functions (large library of 1-arg, 2-arg, 3-arg - functions) i.e.: sin, cos, Stirling numbers, log, inverse functions
- constants (large library), i.e.: pi, e, golden ratio
- n-args functions, i.e.: greatest common divisor
- iterated summation and product operators
- differentiation and integration
- user defined constants and arguments, both free - and dependent on other arguments + possibility of use in functions
- user defined functions (both free and depended)
- user defined recursive arguments + simple (controlled) recursion (1 recursive argument)
- user defined recursive functions / expressions (any) - complex, many arguments, no limitation
- internal syntax checking
- internal help
- other useful functionalities, i.e.: computing time, expression description.
Expression e = new Expression("2+3");
e.calculate();
👍
Expression e = new Expression("2+(3-5)^2");
e.calculate();
👍
Expression e = new Expression("2*pi");
e.calculate();
👍
Constant tau = new Constant("tau = 2*pi");
Expression e = new Expression("3*tau", tau);
e.calculate();
👍
Expression e = new Expression("sin(2*pi)");
e.calculate();
👍
Expression e = new Expression("gcd(2,5,10,30)");
e.calculate();
👍
Argument x = new Argument("x = 5");
Expression e = new Expression("sin(x)", x);
e.calculate();
👍
Argument x = new Argument("x = 5");
Argument y = new Argument("y = 2*x", x);
Expression e = new Expression("sin(y)", y);
e.calculate();
👍
Argument x = new Argument("x = 5");
Expression e = new Expression("if(sin(x) > 5, 1, 0)", x);
e.calculate();
👍
Expression e = new Expression("5=6");
e.calculate();
👍
Expression e = new Expression("5 <= 6");
e.calculate();
👍
Expression e = new Expression("sum(i, 1, 10, 2*i^2 + pi)");
e.calculate();
👍
Expression e = new Expression("prod(i, 1, 5, i, 0.5)");
e.calculate();
👍
Argument x = new Argument("x = pi/2");
Expression e20 = new Expression("sum(n,0,10,(-1)^n*(x^(2*n+1))/(2*n+1)!)", x);
e.calculate();
👍
Argument x = new Argument("x = pi/2");
Expression e = new Expression("cos(x)-der(sin(x), x)", x);
e.calculate();
👍
Expression e = new Expression("2*int(sqrt(1-x^2), x, -1, 1)");
e.calculate();
👍
Function f = new Function("f(x,y) = sin(x) + cos(y)");
f.calculate(1,2);
Expression e = new Expression("f(1,2) - 10", f);
e.calculate();
👍
Function f = new Function("f(n) = if( n>0, n*f(n-1), 1)");
f.calculate()
👍
Function Cnk = new Function("Cnk(n,k) = if(k>0, if(k<n, Cnk(n-1,k-1)+Cnk(n-1,k), 1), 1)");
Cnk.calculate()
👍
Expression e = new Expression("2+1/a");
e.checkSyntax();
mXparser.consolePrintln(e.getErrorMessage());
| Key word | Category | Description | Example | Since |
|---|---|---|---|---|
| Number | Decimal Number | Decimal number | 1, 1.5, -2.3 | 1.0 |
| Number | Decimal Number | Decimal number - scientific notation | 1.2e10, -2.4e-10, 2.3E+10 | 4.0 |
| Number | Binary Number | Binary number - number literal | b.10101, B.10101, b2.10010 | 4.1 |
| Number | Octal Number | Octal number - number literal | o.1027, O.1027, b8.1027 | 4.1 |
| Number | Hexadecimal Number | Hexadecimal number - number literal | h.12fE, H.12fE, b16.12fE | 4.1 |
| Number | Unary Number | Unary number - number literal | b1.111 , B1.111 | 4.1 |
| Number | Base 1-36 | Base 1-36 number - number literal | bN.xxxx , BN.xxxx | 4.1 |
| Number | Fraction | Number literal as fraction | 1_2 , 2_3_4, 172_345, 345_172 | 4.3 |
| Keyword | Type | Syntax | Since | Description |
|---|---|---|---|---|
| + | Operator | a + b | 1.0 | Addition - Operator |
| - | Operator | a - b | 1.0 | Subtraction - Operator |
| * | Operator | a * b | 1.0 | Multiplication - Operator |
| × | Operator | a × b | 5.0 | Multiplication - Operator - Unicode math symbol |
| ⨉ | Operator | a ⨉ b | 5.0 | Multiplication - Operator - Unicode math symbol |
| ∙ | Operator | a ∙ b | 5.0 | Multiplication - Operator - Unicode math symbol |
| / | Operator | a / b | 1.0 | Division - Operator |
| ÷ | Operator | a ÷ b | 5.0 | Division - Operator - Unicode math symbol |
| ^ | Operator | a^b | 1.0 | Exponentiation - Operator |
| ! | Operator | n! | 1.0 | Factorial - Operator |
| # | Operator | a # b | 1.0 | Modulo - Operator |
| % | Operator | n% | 4.1 | Percentage - Operator |
| ^^ | Operator | a^^b | 4.2 | Tetration (hyper-4, power tower, exponential tower) - Operator |
| √ | Operator | √x | 5.0 | Square root - Operator - Unicode math symbol |
| ∛ | Operator | ∛x | 5.0 | Cube root - Operator - Unicode math symbol |
| ∜ | Operator | ∜x | 5.0 | Fourth root - Operator - Unicode math symbol |
| Keyword | Type | Syntax | Since | Description |
|---|---|---|---|---|
| & | Boolean operator | p & q | 1.0 | Logical conjunction AND - Boolean operator |
| ∧ | Boolean operator | p ∧ q | 5.0 | Logical conjunction AND - Boolean operator - Unicode math symbol |
| && | Boolean operator | p && q | 1.0 | Logical conjunction AND - Boolean operator |
| /\ | Boolean operator | p /\ q | 1.0 | Logical conjunction AND - Boolean operator |
| ⊼ | Boolean operator | p ⊼ q | 5.0 | Sheffer stroke NAND - Boolean operator - Unicode math symbol |
| ~& | Boolean operator | p ~& q | 1.0 | Sheffer stroke NAND - Boolean operator |
| ~∧ | Boolean operator | p ~∧ q | 5.0 | Sheffer stroke NAND - Boolean operator - Unicode math symbol |
| ¬& | Boolean operator | p ¬& q | 5.0 | Sheffer stroke NAND - Boolean operator - Unicode math symbol |
| ¬∧ | Boolean operator | p ¬∧ q | 5.0 | Sheffer stroke NAND - Boolean operator - Unicode math symbol |
| ~&& | Boolean operator | p ~&& q | 1.0 | Sheffer stroke NAND - Boolean operator |
| ~/\ | Boolean operator | p ~/\ q | 1.0 | Sheffer stroke NAND - Boolean operator |
| ¬&& | Boolean operator | p ¬&& q | 5.0 | Sheffer stroke NAND - Boolean operator - Unicode math symbol |
| ¬/\ | Boolean operator | p ¬/\ q | 5.0 | Sheffer stroke NAND - Boolean operator - Unicode math symbol |
| | | Boolean operator | p | q | 1.0 | Logical disjunction OR - Boolean operator |
| ∨ | Boolean operator | p ∨ q | 5.0 | Logical disjunction OR - Boolean operator - Unicode math symbol |
| || | Boolean operator | p || q | 1.0 | Logical disjunction OR - Boolean operator |
| \/ | Boolean operator | p \/ q | 1.0 | Logical disjunction OR - Boolean operator |
| ⊽ | Boolean operator | p ⊽ q | 5.0 | Logical not or (joint denial) NOR - Boolean operator - Unicode math symbol |
| ~| | Boolean operator | p ~| q | 1.0 | Logical not or (joint denial) NOR - Boolean operator |
| ~∨ | Boolean operator | p ~∨ q | 5.0 | Logical not or (joint denial) NOR - Boolean operator - Unicode math symbol |
| ¬| | Boolean operator | p ¬| q | 5.0 | Logical not or (joint denial) NOR - Boolean operator - Unicode math symbol |
| ¬∨ | Boolean operator | p ¬∨ q | 5.0 | Logical not or (joint denial) NOR - Boolean operator - Unicode math symbol |
| ~|| | Boolean operator | p ~|| q | 1.0 | Logical not or (joint denial) NOR - Boolean operator |
| ~\/ | Boolean operator | p ~\/ q | 1.0 | Logical not or (joint denial) NOR - Boolean operator |
| ¬|| | Boolean operator | p ¬|| q | 5.0 | Logical not or (joint denial) NOR - Boolean operator - Unicode math symbol |
| ¬\/ | Boolean operator | p ¬\/ q | 5.0 | Logical not or (joint denial) NOR - Boolean operator - Unicode math symbol |
| ⊻ | Boolean operator | p ⊻ q | 5.0 | Exclusive or XOR - Boolean operator - Unicode math symbol |
| (+) | Boolean operator | p (+) q | 1.0 | Exclusive or XOR - Boolean operator |
| ⇒ | Boolean operator | p ⇒ q | 5.0 | Implication IMP - Boolean operator - Unicode math symbol |
| --> | Boolean operator | p --> q | 1.0 | Implication IMP - Boolean operator |
| ⇐ | Boolean operator | p ⇐ q | 5.0 | Converse implication CIMP - Boolean operator - Unicode math symbol |
| <-- | Boolean operator | p <-- q | 1.0 | Converse implication CIMP - Boolean operator |
| ⇏ | Boolean operator | p ⇏ q | 5.0 | Material nonimplication NIMP - Boolean operator - Unicode math symbol |
| -/> | Boolean operator | p -/> q | 1.0 | Material nonimplication NIMP - Boolean operator |
| ⇍ | Boolean operator | p ⇍ q | 5.0 | Converse nonimplication CNIMP - Boolean operator - Unicode math symbol |
| </- | Boolean operator | p </- q | 1.0 | Converse nonimplication CNIMP - Boolean operator |
| ⇔ | Boolean operator | p ⇔ q | 5.0 | Logical biconditional EQV - Boolean operator - Unicode math symbol |
| <-> | Boolean operator | p <-> q | 1.0 | Logical biconditional EQV - Boolean operator |
| ~ | Boolean operator | ~p | 1.0 | Negation - Boolean operator |
| ¬ | Boolean operator | ¬p | 5.0 | Negation - Boolean operator - Unicode math symbol |
| Keyword | Type | Syntax | Since | Description |
|---|---|---|---|---|
| @~ | Bitwise operator | @~a | 4.0 | Bitwise unary complement - Bitwise operator |
| @& | Bitwise operator | a @& b | 4.0 | Bitwise and AND - Bitwise operator |
| @^ | Bitwise operator | a @^ b | 4.0 | Bitwise exclusive or XOR - Bitwise operator |
| @| | Bitwise operator | a @| b | 4.0 | Bitwise inclusive or OR - Bitwise operator |
| @<< | Bitwise operator | a @<< b | 4.0 | Signed left shift - Bitwise operator |
| @>> | Bitwise operator | a @>> b | 4.0 | Signed right shift - Bitwise operator |
| Keyword | Type | Syntax | Since | Description |
|---|---|---|---|---|
| = | Binary relation | a = b | 1.0 | Equality - Binary relation |
| == | Binary relation | a == b | 1.0 | Equality - Binary relation |
| ≠ | Binary relation | a ≠ b | 5.0 | Inequation - Binary relation - Unicode math symbol |
| <> | Binary relation | a <> b | 1.0 | Inequation - Binary relation |
| ~= | Binary relation | a ~= b | 1.0 | Inequation - Binary relation |
| != | Binary relation | a != b | 1.0 | Inequation - Binary relation |
| < | Binary relation | a < b | 1.0 | Lower than - Binary relation |
| > | Binary relation | a > b | 1.0 | Greater than - Binary relation |
| ≤ | Binary relation | a ≤ b | 5.0 | Lower or equal - Binary relation - Unicode math symbol |
| ⋜ | Binary relation | a ⋜ b | 5.0 | Lower or equal - Binary relation - Unicode math symbol |
| <= | Binary relation | a <= b | 1.0 | Lower or equal - Binary relation |
| ≥ | Binary relation | a ≥ b | 5.0 | Greater or equal - Binary relation - Unicode math symbol |
| ⋝ | Binary relation | a ⋝ b | 5.0 | Greater or equal - Binary relation - Unicode math symbol |
| >= | Binary relation | a >= b | 1.0 | Greater or equal - Binary relation |
| Keyword | Type | Syntax | Since | Description |
|---|---|---|---|---|
| sin | Unary function | sin(x) | 1.0 | Trigonometric sine - Unary function |
| cos | Unary function | cos(x) | 1.0 | Trigonometric cosine - Unary function |
| tg | Unary function | tg(x) | 1.0 | Trigonometric tangent - Unary function |
| tan | Unary function | tan(x) | 1.0 | Trigonometric tangent - Unary function |
| ctg | Unary function | ctg(x) | 1.0 | Trigonometric cotangent - Unary function |
| cot | Unary function | cot(x) | 1.0 | Trigonometric cotangent - Unary function |
| ctan | Unary function | ctan(x) | 1.0 | Trigonometric cotangent - Unary function |
| sec | Unary function | sec(x) | 1.0 | Trigonometric secant - Unary function |
| csc | Unary function | csc(x) | 1.0 | Trigonometric cosecant - Unary function |
| cosec | Unary function | cosec(x) | 1.0 | Trigonometric cosecant - Unary function |
| asin | Unary function | asin(x) | 1.0 | Inverse trigonometric sine - Unary function |
| arsin | Unary function | arsin(x) | 1.0 | Inverse trigonometric sine - Unary function |
| arcsin | Unary function | arcsin(x) | 1.0 | Inverse trigonometric sine - Unary function |
| acos | Unary function | acos(x) | 1.0 | Inverse trigonometric cosine - Unary function |
| arcos | Unary function | arcos(x) | 1.0 | Inverse trigonometric cosine - Unary function |
| arccos | Unary function | arccos(x) | 1.0 | Inverse trigonometric cosine - Unary function |
| atg | Unary function | atg(x) | 1.0 | Inverse trigonometric tangent - Unary function |
| atan | Unary function | atan(x) | 1.0 | Inverse trigonometric tangent - Unary function |
| arctg | Unary function | arctg(x) | 1.0 | Inverse trigonometric tangent - Unary function |
| arctan | Unary function | arctan(x) | 1.0 | Inverse trigonometric tangent - Unary function |
| actg | Unary function | actg(x) | 1.0 | Inverse trigonometric cotangent - Unary function |
| acot | Unary function | acot(x) | 1.0 | Inverse trigonometric cotangent - Unary function |
| actan | Unary function | actan(x) | 1.0 | Inverse trigonometric cotangent - Unary function |
| arcctg | Unary function | arcctg(x) | 1.0 | Inverse trigonometric cotangent - Unary function |
| arccot | Unary function | arccot(x) | 1.0 | Inverse trigonometric cotangent - Unary function |
| arcctan | Unary function | arcctan(x) | 1.0 | Inverse trigonometric cotangent - Unary function |
| ln | Unary function | ln(x) | 1.0 | Natural logarithm (base e) - Unary function |
| log2 | Unary function | log2(x) | 1.0 | Binary logarithm (base 2) - Unary function |
| lg | Unary function | lg(x) | 5.0 | Common logarithm (base 10) - Unary function |
| log10 | Unary function | log10(x) | 1.0 | Common logarithm (base 10) - Unary function |
| rad | Unary function | rad(x) | 1.0 | Degrees to radians - Unary function |
| exp | Unary function | exp(x) | 1.0 | Exponential - Unary function |
| sqrt | Unary function | sqrt(x) | 1.0 | Squre root - Unary function |
| sinh | Unary function | sinh(x) | 1.0 | Hyperbolic sine - Unary function |
| cosh | Unary function | cosh(x) | 1.0 | Hyperbolic cosine - Unary function |
| tgh | Unary function | tgh(x) | 1.0 | Hyperbolic tangent - Unary function |
| tanh | Unary function | tanh(x) | 1.0 | Hyperbolic tangent - Unary function |
| coth | Unary function | coth(x) | 1.0 | Hyperbolic cotangent - Unary function |
| ctgh | Unary function | ctgh(x) | 1.0 | Hyperbolic cotangent - Unary function |
| ctanh | Unary function | ctanh(x) | 1.0 | Hyperbolic cotangent - Unary function |
| sech | Unary function | sech(x) | 1.0 | Hyperbolic secant - Unary function |
| csch | Unary function | csch(x) | 1.0 | Hyperbolic cosecant - Unary function |
| cosech | Unary function | cosech(x) | 1.0 | Hyperbolic cosecant - Unary function |
| deg | Unary function | deg(x) | 1.0 | Radians to degrees - Unary function |
| abs | Unary function | abs(x) | 1.0 | Absolut value - Unary function |
| sgn | Unary function | sgn(x) | 1.0 | Signum - Unary function |
| floor | Unary function | floor(x) | 1.0 | Floor - Unary function |
| ceil | Unary function | ceil(x) | 1.0 | Ceiling - Unary function |
| not | Unary function | not(x) | 1.0 | Negation - Unary function |
| asinh | Unary function | asinh(x) | 1.0 | Inverse hyperbolic sine - Unary function |
| arsinh | Unary function | arsinh(x) | 1.0 | Inverse hyperbolic sine - Unary function |
| arcsinh | Unary function | arcsinh(x) | 1.0 | Inverse hyperbolic sine - Unary function |
| acosh | Unary function | acosh(x) | 1.0 | Inverse hyperbolic cosine - Unary function |
| arcosh | Unary function | arcosh(x) | 1.0 | Inverse hyperbolic cosine - Unary function |
| arccosh | Unary function | arccosh(x) | 1.0 | Inverse hyperbolic cosine - Unary function |
| atgh | Unary function | atgh(x) | 1.0 | Inverse hyperbolic tangent - Unary function |
| atanh | Unary function | atanh(x) | 1.0 | Inverse hyperbolic tangent - Unary function |
| arctgh | Unary function | arctgh(x) | 1.0 | Inverse hyperbolic tangent - Unary function |
| arctanh | Unary function | arctanh(x) | 1.0 | Inverse hyperbolic tangent - Unary function |
| acoth | Unary function | acoth(x) | 1.0 | Inverse hyperbolic cotangent - Unary function |
| actgh | Unary function | actgh(x) | 1.0 | Inverse hyperbolic cotangent - Unary function |
| actanh | Unary function | actanh(x) | 1.0 | Inverse hyperbolic cotangent - Unary function |
| arcoth | Unary function | arcoth(x) | 1.0 | Inverse hyperbolic cotangent - Unary function |
| arccoth | Unary function | arccoth(x) | 1.0 | Inverse hyperbolic cotangent - Unary function |
| arcctgh | Unary function | arcctgh(x) | 1.0 | Inverse hyperbolic cotangent - Unary function |
| arcctanh | Unary function | arcctanh(x) | 1.0 | Inverse hyperbolic cotangent - Unary function |
| asech | Unary function | asech(x) | 1.0 | Inverse hyperbolic secant - Unary function |
| arsech | Unary function | arsech(x) | 1.0 | Inverse hyperbolic secant - Unary function |
| arcsech | Unary function | arcsech(x) | 1.0 | Inverse hyperbolic secant - Unary function |
| acsch | Unary function | acsch(x) | 1.0 | Inverse hyperbolic cosecant - Unary function |
| arcsch | Unary function | arcsch(x) | 1.0 | Inverse hyperbolic cosecant - Unary function |
| arccsch | Unary function | arccsch(x) | 1.0 | Inverse hyperbolic cosecant - Unary function |
| acosech | Unary function | acosech(x) | 1.0 | Inverse hyperbolic cosecant - Unary function |
| arcosech | Unary function | arcosech(x) | 1.0 | Inverse hyperbolic cosecant - Unary function |
| arccosech | Unary function | arccosech(x) | 1.0 | Inverse hyperbolic cosecant - Unary function |
| Sa | Unary function | Sa(x) | 1.0 | Sinc (normalized) - Unary function |
| sinc | Unary function | sinc(x) | 1.0 | Sinc (normalized) - Unary function |
| Sinc | Unary function | Sinc(x) | 1.0 | Sinc (unnormalized) - Unary function |
| Bell | Unary function | Bell(n) | 1.0 | Bell number - Unary function |
| Luc | Unary function | Luc(n) | 1.0 | Lucas number - Unary function |
| Fib | Unary function | Fib(n) | 1.0 | Fibonacci number - Unary function |
| harm | Unary function | harm(n) | 1.0 | Harmonic number - Unary function |
| ispr | Unary function | ispr(n) | 2.3 | Prime number test (is number a prime?) - Unary function |
| Pi | Unary function | Pi(n) | 2.3 | Prime-counting π(n) - Unary function |
| Ei | Unary function | Ei(x) | 2.3 | Exponential integral - Special function Ei(x) - Unary function |
| li | Unary function | li(x) | 2.3 | Logarithmic integral - Special function li(x) - Unary function |
| Li | Unary function | Li(x) | 2.3 | Offset logarithmic integral - Special function Li(x) - Unary function |
| erf | Unary function | erf(x) | 3.0 | Gauss error - Special function erf(x) - Unary function |
| erfc | Unary function | erfc(x) | 3.0 | Gauss complementary error - Special function erfc(x) - Unary function |
| erfInv | Unary function | erfInv(x) | 3.0 | Inverse Gauss error - Special function erf⁻¹(y) - Unary function |
| erfcInv | Unary function | erfcInv(x) | 3.0 | Inverse Gauss complementary error - Special function erfc⁻¹(x) - Unary function |
| ulp | Unary function | ulp(x) | 3.0 | Unit in The Last Place - Unary function |
| isNaN | Unary function | isNaN(x) | 4.1 | Returns true if value is a Not-a-Number (NaN), false otherwise (true=1, false=1) - Unary function |
| ndig10 | Unary function | ndig10(x) | 4.1 | Number of digits in numeral system with base 10 - Unary function |
| nfact | Unary function | nfact(x) | 4.1 | Prime decomposition - number of distinct prime factors - Unary function |
| arcsec | Unary function | arcsec(x) | 4.1 | Inverse trigonometric secant - Unary function |
| arccsc | Unary function | arccsc(x) | 4.1 | Inverse trigonometric cosecant - Unary function |
| Gamma | Unary function | Gamma(x) | 4.2 | Gamma - Special function Γ(s) - Unary function |
| LambW0 | Unary function | LambW0(x) | 4.2 | Lambert-W, principal branch 0, also called the omega or product logarithm - Special function W₀(x) - Unary function |
| LambW1 | Unary function | LambW1(x) | 4.2 | Lambert-W, branch -1, also called the omega or product logarithm - Special function W₋₁(x) - Unary function |
| sgnGamma | Unary function | sgnGamma(x) | 4.2 | Signum of Gamma - Special function Γ(s) - Unary function |
| logGamma | Unary function | logGamma(x) | 4.2 | Log Gamma - Special function lnΓ(s) - Unary function |
| diGamma | Unary function | diGamma(x) | 4.2 | Digamma as the logarithmic derivative of the Gamma - Special function ψ(x) - Unary function |
| rStud | Unary function | rStud(v) | 5.0 | Random variable - Student's t-distribution - Unary function |
| rChi2 | Unary function | rChi2(k) | 5.0 | Random variable - Chi-squared distribution - Unary function |
| Keyword | Type | Syntax | Since | Description |
|---|---|---|---|---|
| log | Binary function | log(a, b) | 1.0 | Logarithm - Binary function |
| mod | Binary function | mod(a, b) | 1.0 | Modulo - Binary function |
| C | Binary function | C(n, k) | 1.0 | Binomial coefficient, number of k-combinations that can be drawn from n-elements set - Binary function |
| nCk | Binary function | nCk(n, k) | 4.2 | Binomial coefficient, number of k-combinations that can be drawn from n-elements set - Binary function |
| Bern | Binary function | Bern(m, n) | 1.0 | Bernoulli numbers - Binary function |
| Stirl1 | Binary function | Stirl1(n, k) | 1.0 | Stirling numbers of the first kind - Binary function |
| Stirl2 | Binary function | Stirl2(n, k) | 1.0 | Stirling numbers of the second kind - Binary function |
| Worp | Binary function | Worp(n, k) | 1.0 | Worpitzky number - Binary function |
| Euler | Binary function | Euler(n, k) | 1.0 | Euler number - Binary function |
| KDelta | Binary function | KDelta(i, j) | 1.0 | Kronecker delta - Binary function |
| EulerPol | Binary function | EulerPol(m, x) | 1.0 | Euler polynomial - Binary function |
| Harm | Binary function | Harm(x, n) | 1.0 | Harmonic number - Binary function |
| rUni | Binary function | rUni(a, b) | 3.0 | Random variable - Uniform continuous distribution U(a,b) - Binary function |
| rUnid | Binary function | rUnid(a, b) | 3.0 | Random variable - Uniform discrete distribution U{a,b} - Binary function |
| round | Binary function | round(x, n) | 3.0 | Half-up rounding - Binary function |
| rNor | Binary function | rNor(mean, stdv) | 3.0 | Random variable - Normal distribution N(μ,σ) - Binary function |
| ndig | Binary function | ndig(number, base) | 4.1 | Number of digits representing the number in numeral system with given base - Binary function |
| dig10 | Binary function | dig10(num, pos) | 4.1 | Digit at position 1 ... n (left -> right) or 0 ... -(n-1) (right -> left) - base 10 numeral system - Binary function |
| factval | Binary function | factval(number, factorid) | 4.1 | Prime decomposition - factor value at position between 1 ... nfact(n) - ascending order by factor value - Binary function |
| factexp | Binary function | factexp(number, factorid) | 4.1 | Prime decomposition - factor exponent / multiplicity at position between 1 ... nfact(n) - ascending order by factor value - Binary function |
| root | Binary function | root(rootorder, number) | 4.1 | N-th order root of a number - Binary function |
| GammaL | Binary function | GammaL(s, x) | 4.2 | Lower incomplete gamma - Special function γ(s,x) - Binary function |
| GammaU | Binary function | GammaU(s, x) | 4.2 | Upper incomplete Gamma - Special function Γ(s,x) - Binary function |
| GammaP | Binary function | GammaP(s, x) | 4.2 | Lower regularized P gamma - Special function P(s,x) - Binary function |
| GammaRegL | Binary function | GammaRegL(s, x) | 4.2 | Lower regularized P gamma - Special function P(s,x) - Binary function |
| GammaQ | Binary function | GammaQ(s, x) | 4.2 | Upper regularized Q Gamma - Special function Q(s,x) - Binary function |
| GammaRegU | Binary function | GammaRegU(s, x) | 4.2 | Upper regularized Q Gamma - Special function Q(s,x) - Binary function |
| nPk | Binary function | nPk(n, k) | 4.2 | Number of k-permutations that can be drawn from n-elements set - Binary function |
| Beta | Binary function | Beta(x, y) | 4.2 | The Beta, also called the Euler integral of the first kind - Special function B(x,y) - Binary function |
| logBeta | Binary function | logBeta(x, y) | 4.2 | The Log Beta, also called the Log Euler integral of the first kind - Special function lnB(x,y) - Binary function |
| pStud | Binary function | pStud(x, v) | 5.0 | Student's t-distribution - Probability distribution function - Binary function |
| cStud | Binary function | cStud(x, v) | 5.0 | Student's t-distribution - Cumulative distribution function - Binary function |
| qStud | Binary function | qStud(p, v) | 5.0 | Student's t-distribution - Quantile function (inverse cumulative distribution function) - Binary function |
| pChi2 | Binary function | pChi2(x, k) | 5.0 | Chi-squared distribution - Probability distribution function - Binary function |
| cChi2 | Binary function | cChi2(x, k) | 5.0 | Chi-squared distribution - Cumulative distribution function - Binary function |
| qChi2 | Binary function | qChi2(p, k) | 5.0 | Chi-squared distribution - Quantile function (inverse cumulative distribution function) - Binary function |
| rFSned | Binary function | rFSned(d1, d2) | 5.1 | Random variable - Snedecor's F distribution (F-distribution or F-ratio, also known as Fisher–Snedecor distribution) - Binary function |
| Keyword | Type | Syntax | Since | Description |
|---|---|---|---|---|
| if | Ternary function | if(cond, expr-if-true, expr-if-false) | 1.0 | If - Ternary function |
| chi | Ternary function | chi(x, a, b) | 1.0 | Characteristic function for x in (a,b) - Ternary function |
| CHi | Ternary function | CHi(x, a, b) | 1.0 | Characteristic function for x in [a,b] - Ternary function |
| Chi | Ternary function | Chi(x, a, b) | 1.0 | Characteristic function for x in [a,b) - Ternary function |
| cHi | Ternary function | cHi(x, a, b) | 1.0 | Characteristic function for x in (a,b] - Ternary function |
| pUni | Ternary function | pUni(x, a, b) | 3.0 | Uniform continuous distribution - Probability distribution function U(a,b) - Ternary function |
| cUni | Ternary function | cUni(a, a, b) | 3.0 | Uniform continuous distribution - Cumulative distribution function U(a,b) - Ternary function |
| qUni | Ternary function | qUni(q, a, b) | 3.0 | Uniform continuous distribution - Quantile function (inverse cumulative distribution function) U(a,b) - Ternary function |
| pNor | Ternary function | pNor(x, mean, stdv) | 3.0 | Normal distribution - Probability distribution function N(μ,σ) - Ternary function |
| cNor | Ternary function | cNor(x, mean, stdv) | 3.0 | Normal distribution - Cumulative distribution function N(μ,σ) - Ternary function |
| qNor | Ternary function | qNor(q, mean, stdv) | 3.0 | Normal distribution - Quantile function (inverse cumulative distribution function) N(μ,σ) - Ternary function |
| dig | Ternary function | dig(num, pos, base) | 4.1 | Digit at position 1 ... n (left -> right) or 0 ... -(n-1) (right -> left) - numeral system with given base - Ternary function |
| BetaInc | Ternary function | BetaInc(x, a, b) | 4.2 | The incomplete Beta, also called the incomplete Euler integral of the first kind - Special function B(x,a,b) - Ternary function |
| BetaI | Ternary function | BetaI(x, a, b) | 4.2 | The regularized incomplete Beta (or regularized beta), also called the regularized incomplete Euler integral of the first kind - Special function I(x,a,b) - Ternary function |
| BetaReg | Ternary function | BetaReg(x, a, b) | 4.2 | The regularized incomplete Beta (or regularized beta), also called the regularized incomplete Euler integral of the first kind - Special function I(x,a,b) - Ternary function |
| pFSned | Ternary function | pFSned(x, d1, d2) | 5.1 | Snedecor's F distribution (F-distribution or F-ratio, also known as Fisher–Snedecor distribution) - Probability distribution function - Ternary function |
| cFSned | Ternary function | cFSned(x, d1, d2) | 5.1 | Snedecor's F distribution (F-distribution or F-ratio, also known as Fisher–Snedecor distribution) - Cumulative distribution function - Ternary function |
| qFSned | Ternary function | qFSned(p, d1, d2) | 5.1 | Snedecor's F distribution (F-distribution or F-ratio, also known as Fisher–Snedecor distribution) - Quantile function (inverse cumulative distribution function) - Ternary function |
| Keyword | Type | Syntax | Since | Description |
|---|---|---|---|---|
| iff | Variadic function | iff(cond-1, expr-1; ... ; cond-n, expr-n) | 1.0 | If function - Variadic function |
| min | Variadic function | min(a1, ..., an) | 1.0 | Minimum - Variadic function |
| max | Variadic function | max(a1, ..., an) | 1.0 | Maximum - Variadic function |
| ConFrac | Variadic function | ConFrac(a1, ..., an) | 1.0 | Continued fraction - Variadic function |
| ConPol | Variadic function | ConPol(a1, ..., an) | 1.0 | Continued polynomial - Variadic function |
| gcd | Variadic function | gcd(a1, ..., an) | 1.0 | Greatest common divisor - Variadic function |
| lcm | Variadic function | lcm(a1, ..., an) | 1.0 | Least common multiple - Variadic function |
| add | Variadic function | add(a1, ..., an) | 2.4 | Summation - Variadic function |
| multi | Variadic function | multi(a1, ..., an) | 2.4 | Multiplication - Variadic function |
| mean | Variadic function | mean(a1, ..., an) | 2.4 | Mean / average value - Variadic function |
| var | Variadic function | var(a1, ..., an) | 2.4 | Bias-corrected sample variance - Variadic function |
| std | Variadic function | std(a1, ..., an) | 2.4 | Bias-corrected sample standard deviation - Variadic function |
| rList | Variadic function | rList(a1, ..., an) | 3.0 | Random number from a given list of numbers - Variadic function |
| coalesce | Variadic function | coalesce(a1, ..., an) | 4.1 | Returns the first non-NaN value - Variadic function |
| or | Variadic function | or(a1, ..., an) | 4.1 | Logical disjunction (OR) - variadic - Variadic function |
| and | Variadic function | and(a1, ..., an) | 4.1 | Logical conjunction (AND) - variadic - Variadic function |
| xor | Variadic function | xor(a1, ..., an) | 4.1 | Exclusive or (XOR) - variadic - Variadic function |
| argmin | Variadic function | argmin(a1, ..., an) | 4.1 | Arguments / indices of the minima - Variadic function |
| argmax | Variadic function | argmax(a1, ..., an) | 4.1 | Arguments / indices of the maxima - Variadic function |
| med | Variadic function | med(a1, ..., an) | 4.1 | The sample median - Variadic function |
| mode | Variadic function | mode(a1, ..., an) | 4.1 | Mode - the value that appears most often - Variadic function |
| base | Variadic function | base(b, d1, ..., dn) | 4.1 | Returns number in given numeral system base represented by list of digits - Variadic function |
| ndist | Variadic function | ndist(v1, ..., vn) | 4.1 | Number of distinct values - Variadic function |
| Keyword | Type | Syntax | Since | Description |
|---|---|---|---|---|
| ∑ | Calculus operator | ∑(i, from, to, expr, ) | 5.0 | Summation SIGMA - Iterated operator Σ - Calculus operator - Unicode math symbol |
| Σ | Calculus operator | Σ(i, from, to, expr, ) | 5.0 | Summation SIGMA - Iterated operator Σ - Calculus operator - Unicode math symbol |
| sum | Calculus operator | sum(i, from, to, expr, ) | 1.0 | Summation SIGMA - Iterated operator Σ - Calculus operator |
| ∏ | Calculus operator | ∏(i, from, to, expr, ) | 5.0 | Product PI - Iterated operator ∏ - Calculus operator - Unicode math symbol |
| ℿ | Calculus operator | ℿ(i, from, to, expr, ) | 5.0 | Product PI - Iterated operator ∏ - Calculus operator - Unicode math symbol |
| Π | Calculus operator | Π(i, from, to, expr, ) | 5.0 | Product PI - Iterated operator ∏ - Calculus operator - Unicode math symbol |
| prod | Calculus operator | prod(i, from, to, expr, ) | 1.0 | Product PI - Iterated operator ∏ - Calculus operator |
| ∫ | Calculus operator | ∫(expr, arg, from, to) | 5.0 | Definite integral ∫ - Calculus operator - Unicode math symbol |
| int | Calculus operator | int(expr, arg, from, to) | 1.0 | Definite integral ∫ - Calculus operator |
| ∂ | Calculus operator | ∂(expr, arg, ) | 5.0 | Derivative ∂ - Calculus operator - Unicode math symbol |
| der | Calculus operator | der(expr, arg, ) | 1.0 | Derivative ∂ - Calculus operator |
| ∂- | Calculus operator | ∂-(expr, arg, ) | 5.0 | Left derivative ∂- - Calculus operator - Unicode math symbol |
| der- | Calculus operator | der-(expr, arg, ) | 1.0 | Left derivative ∂- - Calculus operator |
| ∂+ | Calculus operator | ∂+(expr, arg, ) | 5.0 | Right derivative ∂+ - Calculus operator - Unicode math symbol |
| der+ | Calculus operator | der+(expr, arg, ) | 1.0 | Right derivative ∂+ - Calculus operator |
| dern | Calculus operator | dern(expr, n, arg) | 1.0 | n-th derivative ∂ⁿ - Calculus operator |
| ∆ | Calculus operator | ∆(expr, arg, ) | 5.0 | Forward difference ∆ - Calculus operator - Unicode math symbol |
| Δ | Calculus operator | Δ(expr, arg, ) | 5.0 | Forward difference ∆ - Calculus operator - Unicode math symbol |
| diff | Calculus operator | diff(expr, arg, ) | 1.0 | Forward difference ∆ - Calculus operator |
| ∇ | Calculus operator | ∇(expr, arg, ) | 5.0 | Backward difference ∇ - Calculus operator - Unicode math symbol |
| difb | Calculus operator | difb(expr, arg, ) | 1.0 | Backward difference ∇ - Calculus operator |
| avg | Calculus operator | avg(i, from, to, expr, ) | 2.4 | Average - Iterated operator - Calculus operator |
| vari | Calculus operator | vari(i, from, to, expr, ) | 2.4 | Bias-corrected sample variance - Iterated operator - Calculus operator |
| stdi | Calculus operator | stdi(i, from, to, expr, ) | 2.4 | Bias-corrected sample standard deviation - Iterated operator - Calculus operator |
| mini | Calculus operator | mini(i, from, to, expr, ) | 2.4 | Minimum value - Iterated operator - Calculus operator |
| maxi | Calculus operator | maxi(i, from, to, expr, ) | 2.4 | Maximum value - Iterated operator - Calculus operator |
| solve | Calculus operator | solve(expr, arg, from, to) | 4.0 | Equation solving (root finding) f(x)=0 - Calculus operator |
| Keyword | Type | Syntax | Since | Description |
|---|---|---|---|---|
| [Uni] | Random variable | [Uni] | 3.0 | Uniform continuous distribution U(0,1) - Random variable |
| [Int] | Random variable | [Int] | 3.0 | Random integer - Random variable |
| [Int1] | Random variable | [Int1] | 3.0 | Uniform discrete distribution - Random integer U{-10¹,10¹} - Random variable |
| [Int2] | Random variable | [Int2] | 3.0 | Uniform discrete distribution - Random integer U{-10²,10²} - Random variable |
| [Int3] | Random variable | [Int3] | 3.0 | Uniform discrete distribution - Random integer U{-10³,10³} - Random variable |
| [Int4] | Random variable | [Int4] | 3.0 | Uniform discrete distribution - Random integer U{-10⁴,10⁴} - Random variable |
| [Int5] | Random variable | [Int5] | 3.0 | Uniform discrete distribution - Random integer U{-10⁵,10⁵} - Random variable |
| [Int6] | Random variable | [Int6] | 3.0 | Uniform discrete distribution - Random integer U{-10⁶,10⁶} - Random variable |
| [Int7] | Random variable | [Int7] | 3.0 | Uniform discrete distribution - Random integer U{-10⁷,10⁷} - Random variable |
| [Int8] | Random variable | [Int8] | 3.0 | Uniform discrete distribution - Random integer U{-10⁸,10⁸} - Random variable |
| [Int9] | Random variable | [Int9] | 3.0 | Uniform discrete distribution - Random integer U{-10⁹,10⁹} - Random variable |
| [nat] | Random variable | [nat] | 3.0 | Random natural number including 0 - Random variable |
| [nat1] | Random variable | [nat1] | 3.0 | Uniform discrete distribution - Random natural number including 0 U{0,10¹} - Random variable |
| [nat2] | Random variable | [nat2] | 3.0 | Uniform discrete distribution - Random natural number including 0 U{0,10²} - Random variable |
| [nat3] | Random variable | [nat3] | 3.0 | Uniform discrete distribution - Random natural number including 0 U{0,10³} - Random variable |
| [nat4] | Random variable | [nat4] | 3.0 | Uniform discrete distribution - Random natural number including 0 U{0,10⁴} - Random variable |
| [nat5] | Random variable | [nat5] | 3.0 | Uniform discrete distribution - Random natural number including 0 U{0,10⁵} - Random variable |
| [nat6] | Random variable | [nat6] | 3.0 | Uniform discrete distribution - Random natural number including 0 U{0,10⁶} - Random variable |
| [nat7] | Random variable | [nat7] | 3.0 | Uniform discrete distribution - Random natural number including 0 U{0,10⁷} - Random variable |
| [nat8] | Random variable | [nat8] | 3.0 | Uniform discrete distribution - Random natural number including 0 U{0,10⁸} - Random variable |
| [nat9] | Random variable | [nat9] | 3.0 | Uniform discrete distribution - Random natural number including 0 U{0,10⁹} - Random variable |
| [Nat] | Random variable | [Nat] | 3.0 | Random natural number - Random variable |
| [Nat1] | Random variable | [Nat1] | 3.0 | Uniform discrete distribution - Random natural number U{1,10¹} - Random variable |
| [Nat2] | Random variable | [Nat2] | 3.0 | Uniform discrete distribution - Random natural number U{1,10²} - Random variable |
| [Nat3] | Random variable | [Nat3] | 3.0 | Uniform discrete distribution - Random natural number U{1,10³} - Random variable |
| [Nat4] | Random variable | [Nat4] | 3.0 | Uniform discrete distribution - Random natural number U{1,10⁴} - Random variable |
| [Nat5] | Random variable | [Nat5] | 3.0 | Uniform discrete distribution - Random natural number U{1,10⁵} - Random variable |
| [Nat6] | Random variable | [Nat6] | 3.0 | Uniform discrete distribution - Random natural number U{1,10⁶} - Random variable |
| [Nat7] | Random variable | [Nat7] | 3.0 | Uniform discrete distribution - Random natural number U{1,10⁷} - Random variable |
| [Nat8] | Random variable | [Nat8] | 3.0 | Uniform discrete distribution - Random natural number U{1,10⁸} - Random variable |
| [Nat9] | Random variable | [Nat9] | 3.0 | Uniform discrete distribution - Random natural number U{1,10⁹} - Random variable |
| [Nor] | Random variable | [Nor] | 3.0 | Normal distribution N(0,1) - Random variable |
| Keyword | Type | Syntax | Since | Description |
|---|---|---|---|---|
| π | Constant value | π | 5.0 | Pi, Archimedes' or Ludolph's number - Mathematical constant π - Constant value - Unicode math symbol |
| ℼ | Constant value | ℼ | 5.0 | Pi, Archimedes' or Ludolph's number - Mathematical constant π - Constant value - Unicode math symbol |
| pi | Constant value | pi | 1.0 | Pi, Archimedes' or Ludolph's number - Mathematical constant π - Constant value |
| e | Constant value | e | 1.0 | Napier's or Euler's number (base of Natural logarithm) - Mathematical constant e - Constant value |
| ℯ | Constant value | ℯ | 5.0 | Napier's or Euler's number (base of Natural logarithm) - Mathematical constant e - Constant value - Unicode math symbol |
| ⅇ | Constant value | ⅇ | 5.0 | Napier's or Euler's number (base of Natural logarithm) - Mathematical constant e - Constant value - Unicode math symbol |
| [gam] | Constant value | [gam] | 1.0 | Euler-Mascheroni constant - Mathematical constant γ - Constant value |
| [phi] | Constant value | [phi] | 1.0 | Golden ratio - Mathematical constant φ - Constant value |
| [PN] | Constant value | [PN] | 1.0 | Plastic constant - Mathematical constant ρ - Constant value |
| [B*] | Constant value | [B*] | 1.0 | Embree-Trefethen constant - Mathematical constant β* - Constant value |
| [F'd] | Constant value | [F'd] | 1.0 | Feigenbaum delta constant - Mathematical constant δ - Constant value |
| [F'a] | Constant value | [F'a] | 1.0 | Feigenbaum alpha constant - Mathematical constant α - Constant value |
| [C2] | Constant value | [C2] | 1.0 | Twin prime constant - Mathematical constant ∏₂ - Constant value |
| [M1] | Constant value | [M1] | 1.0 | Meissel-Mertens constant - Mathematical constant M₁, B₁ - Constant value |
| [B2] | Constant value | [B2] | 1.0 | Brun's constant for twin primes - Mathematical constant B₂ - Constant value |
| [B4] | Constant value | [B4] | 1.0 | Brun's constant for prime quadruplets - Mathematical constant B₄ - Constant value |
| [BN'L] | Constant value | [BN'L] | 1.0 | de Bruijn-Newman constant - Mathematical constant Λ - Constant value |
| [Kat] | Constant value | [Kat] | 1.0 | Catalan's constant - Mathematical constant G - Constant value |
| [K*] | Constant value | [K*] | 1.0 | Landau-Ramanujan constant - Mathematical constant b - Constant value |
| [K.] | Constant value | [K.] | 1.0 | Viswanath's constant - Mathematical constant V - Constant value |
| [B'L] | Constant value | [B'L] | 1.0 | Legendre's constant - Mathematical constant B - Constant value |
| [RS'm] | Constant value | [RS'm] | 1.0 | Ramanujan-Soldner constant - Mathematical constant μ - Constant value |
| [EB'e] | Constant value | [EB'e] | 1.0 | Erdos-Borwein constant - Mathematical constant E - Constant value |
| [Bern] | Constant value | [Bern] | 1.0 | Bernstein's constant - Mathematical constant β - Constant value |
| [GKW'l] | Constant value | [GKW'l] | 1.0 | Gauss-Kuzmin-Wirsing constant - Mathematical constant λ - Constant value |
| [HSM's] | Constant value | [HSM's] | 1.0 | Hafner-Sarnak-McCurley constant - Mathematical constant σ - Constant value |
| [lm] | Constant value | [lm] | 1.0 | Golomb-Dickman constant - Mathematical constant λ - Constant value |
| [Cah] | Constant value | [Cah] | 1.0 | Cahen's constant - Mathematical constant C - Constant value |
| [Ll] | Constant value | [Ll] | 1.0 | Laplace limit constant - Mathematical constant - Constant value |
| [AG] | Constant value | [AG] | 1.0 | Alladi-Grinstead constant - Mathematical constant - Constant value |
| [L*] | Constant value | [L*] | 1.0 | Lengyel's constant - Mathematical constant Λ - Constant value |
| [L.] | Constant value | [L.] | 1.0 | Levy's constant - Mathematical constant - Constant value |
| [Dz3] | Constant value | [Dz3] | 1.0 | Apery's constant - Mathematical constant ζ(3) - Constant value |
| [A3n] | Constant value | [A3n] | 1.0 | Mills' constant - Mathematical constant A - Constant value |
| [Bh] | Constant value | [Bh] | 1.0 | Backhouse's constant - Mathematical constant B - Constant value |
| [Pt] | Constant value | [Pt] | 1.0 | Porter's constant - Mathematical constant C - Constant value |
| [L2] | Constant value | [L2] | 1.0 | Lieb's square ice constant - Mathematical constant - Constant value |
| [Nv] | Constant value | [Nv] | 1.0 | Niven's constant - Mathematical constant C - Constant value |
| [Ks] | Constant value | [Ks] | 1.0 | Sierpinski's constant - Mathematical constant K - Constant value |
| [Kh] | Constant value | [Kh] | 1.0 | Khinchin's constant - Mathematical constant K₀ - Constant value |
| [FR] | Constant value | [FR] | 1.0 | Fransen-Robinson constant - Mathematical constant F - Constant value |
| [La] | Constant value | [La] | 1.0 | Landau's constant - Mathematical constant L - Constant value |
| [P2] | Constant value | [P2] | 1.0 | Parabolic constant - Mathematical constant P - Constant value |
| [Om] | Constant value | [Om] | 1.0 | Omega constant - Mathematical constant Ω - Constant value |
| [MRB] | Constant value | [MRB] | 1.0 | MRB constant - Mathematical constant S - Constant value |
| [li2] | Constant value | [li2] | 2.3 | Logarithmic integral at point 2 - Mathematical constant li(2) - Constant value |
| [EG] | Constant value | [EG] | 2.3 | Gompertz constant - Mathematical constant δ - Constant value |
| Keyword | Type | Syntax | Since | Description |
|---|---|---|---|---|
| [c] | Constant value | [c] | 4.0 | Light speed in vacuum - Physical constant c [m/s] (m=1, s=1) - Constant value |
| [G.] | Constant value | [G.] | 4.0 | Gravitational constant - Physical constant G (m=1, kg=1, s=1) - Constant value |
| [g] | Constant value | [g] | 4.0 | Gravitational acceleration on Earth - Physical constant g [m/s²] (m=1, s=1) - Constant value |
| [hP] | Constant value | [hP] | 4.0 | Planck constant - Physical constant h (m=1, kg=1, s=1) - Constant value |
| [h-] | Constant value | [h-] | 4.0 | Reduced Planck constant (Dirac constant) - Physical constant ħ (m=1, kg=1, s=1) - Constant value |
| [lP] | Constant value | [lP] | 4.0 | Planck length - Physical constant lᵖ [m] (m=1) - Constant value |
| [mP] | Constant value | [mP] | 4.0 | Planck mass - Physical constant mᵖ [kg] (kg=1) - Constant value |
| [tP] | Constant value | [tP] | 4.0 | Planck time - Physical constant tᵖ [s] (s=1) - Constant value |
| Keyword | Type | Syntax | Since | Description |
|---|---|---|---|---|
| [ly] | Constant value | [ly] | 4.0 | Light year - Astronomical constant ly [m] (m=1) - Constant value |
| [au] | Constant value | [au] | 4.0 | Astronomical unit - Astronomical constant au, AU [m] (m=1) - Constant value |
| [pc] | Constant value | [pc] | 4.0 | Parsec - Astronomical constant pc [m] (m=1) - Constant value |
| [kpc] | Constant value | [kpc] | 4.0 | Kiloparsec - Astronomical constant kpc [m] (m=1) - Constant value |
| [Earth-R-eq] | Constant value | [Earth-R-eq] | 4.0 | Earth equatorial radius - Astronomical constant Rª⊕ [m] (m=1) - Constant value |
| [Earth-R-po] | Constant value | [Earth-R-po] | 4.0 | Earth polar radius - Astronomical constant Rᵇ⊕ [m] (m=1) - Constant value |
| [Earth-R] | Constant value | [Earth-R] | 4.0 | Earth mean radius - Astronomical constant R⊕ (m=1) - Constant value |
| [Earth-M] | Constant value | [Earth-M] | 4.0 | Earth mass - Astronomical constant M⊕ [kg] (kg=1) - Constant value |
| [Earth-D] | Constant value | [Earth-D] | 4.0 | Earth-Sun distance - Astronomical constant - Semi major axis [m] (m=1) - Constant value |
| [Moon-R] | Constant value | [Moon-R] | 4.0 | Moon mean radius - Astronomical constant [m] (m=1) - Constant value |
| [Moon-M] | Constant value | [Moon-M] | 4.0 | Moon mass - Astronomical constant [kg] (kg=1) - Constant value |
| [Moon-D] | Constant value | [Moon-D] | 4.0 | Moon-Earth distance - Astronomical constant - Semi major axis [m] (m=1) - Constant value |
| [Solar-R] | Constant value | [Solar-R] | 4.0 | Solar mean radius - Astronomical constant R☉ [m] (m=1) - Constant value |
| [Solar-M] | Constant value | [Solar-M] | 4.0 | Solar mass - Astronomical constant M☉ [kg] (kg=1) - Constant value |
| [Mercury-R] | Constant value | [Mercury-R] | 4.0 | Mercury mean radius - Astronomical constant [m] (m=1) - Constant value |
| [Mercury-M] | Constant value | [Mercury-M] | 4.0 | Mercury mass - Astronomical constant [kg] (kg=1) - Constant value |
| [Mercury-D] | Constant value | [Mercury-D] | 4.0 | Mercury-Sun distance - Astronomical constant - Semi major axis [m] (m=1) - Constant value |
| [Venus-R] | Constant value | [Venus-R] | 4.0 | Venus mean radius - Astronomical constant [m] (m=1) - Constant value |
| [Venus-M] | Constant value | [Venus-M] | 4.0 | Venus mass - Astronomical constant [kg] (kg=1) - Constant value |
| [Venus-D] | Constant value | [Venus-D] | 4.0 | Venus-Sun distance - Astronomical constant - Semi major axis [m] (m=1) - Constant value |
| [Mars-R] | Constant value | [Mars-R] | 4.0 | Mars mean radius - Astronomical constant [m] (m=1) - Constant value |
| [Mars-M] | Constant value | [Mars-M] | 4.0 | Mars mass - Astronomical constant [kg] (kg=1) - Constant value |
| [Mars-D] | Constant value | [Mars-D] | 4.0 | Mars-Sun distance - Astronomical constant - Semi major axis [m] (m=1) - Constant value |
| [Jupiter-R] | Constant value | [Jupiter-R] | 4.0 | Jupiter mean radius - Astronomical constant [m] (m=1) - Constant value |
| [Jupiter-M] | Constant value | [Jupiter-M] | 4.0 | Jupiter mass - Astronomical constant [kg] (kg=1) - Constant value |
| [Jupiter-D] | Constant value | [Jupiter-D] | 4.0 | Jupiter-Sun distance - Astronomical constant - Semi major axis [m] (m=1) - Constant value |
| [Saturn-R] | Constant value | [Saturn-R] | 4.0 | Saturn mean radius - Astronomical constant [m] (m=1) - Constant value |
| [Saturn-M] | Constant value | [Saturn-M] | 4.0 | Saturn mass - Astronomical constant [kg] (kg=1) - Constant value |
| [Saturn-D] | Constant value | [Saturn-D] | 4.0 | Saturn-Sun distance - Astronomical constant - Semi major axis [m] (m=1) - Constant value |
| [Uranus-R] | Constant value | [Uranus-R] | 4.0 | Uranus mean radius - Astronomical constant [m] (m=1) - Constant value |
| [Uranus-M] | Constant value | [Uranus-M] | 4.0 | Uranus mass - Astronomical constant [kg] (kg=1) - Constant value |
| [Uranus-D] | Constant value | [Uranus-D] | 4.0 | Uranus-Sun distance - Astronomical constant - Semi major axis [m] (m=1) - Constant value |
| [Neptune-R] | Constant value | [Neptune-R] | 4.0 | Neptune mean radius - Astronomical constant [m] (m=1) - Constant value |
| [Neptune-M] | Constant value | [Neptune-M] | 4.0 | Neptune mass - Astronomical constant [kg] (kg=1) - Constant value |
| [Neptune-D] | Constant value | [Neptune-D] | 4.0 | Neptune-Sun distance - Astronomical constant - Semi major axis [m] (m=1) - Constant value |
| Keyword | Type | Syntax | Since | Description |
|---|---|---|---|---|
| [Y] | Unit | [Y] | 4.0 | Septillion / Yotta - Metric prefix = 10²⁴ - Dimensionless unit |
| [sept] | Unit | [sept] | 4.0 | Septillion / Yotta - Metric prefix = 10²⁴ - Dimensionless unit |
| [Z] | Unit | [Z] | 4.0 | Sextillion / Zetta - Metric prefix = 10²¹ - Dimensionless unit |
| [sext] | Unit | [sext] | 4.0 | Sextillion / Zetta - Metric prefix = 10²¹ - Dimensionless unit |
| [E] | Unit | [E] | 4.0 | Quintillion / Exa - Metric prefix = 10¹⁸ - Dimensionless unit |
| [quint] | Unit | [quint] | 4.0 | Quintillion / Exa - Metric prefix = 10¹⁸ - Dimensionless unit |
| [P] | Unit | [P] | 4.0 | Quadrillion / Peta - Metric prefix = 10¹⁵ - Dimensionless unit |
| [quad] | Unit | [quad] | 4.0 | Quadrillion / Peta - Metric prefix = 10¹⁵ - Dimensionless unit |
| [T] | Unit | [T] | 4.0 | Trillion / Tera - Metric prefix = 10¹² - Dimensionless unit |
| [tril] | Unit | [tril] | 4.0 | Trillion / Tera - Metric prefix = 10¹² - Dimensionless unit |
| [G] | Unit | [G] | 4.0 | Billion / Giga - Metric prefix = 10⁹ - Dimensionless unit |
| [bil] | Unit | [bil] | 4.0 | Billion / Giga - Metric prefix = 10⁹ - Dimensionless unit |
| [M] | Unit | [M] | 4.0 | Million / Mega - Metric prefix = 10⁶ - Dimensionless unit |
| [mil] | Unit | [mil] | 4.0 | Million / Mega - Metric prefix = 10⁶ - Dimensionless unit |
| [k] | Unit | [k] | 4.0 | Thousand / Kilo - Metric prefix = 10³ - Dimensionless unit |
| [th] | Unit | [th] | 4.0 | Thousand / Kilo - Metric prefix = 10³ - Dimensionless unit |
| [hund] | Unit | [hund] | 4.0 | Hundred / Hecto - Metric prefix = 10² - Dimensionless unit |
| [hecto] | Unit | [hecto] | 4.0 | Hundred / Hecto - Metric prefix = 10² - Dimensionless unit |
| [ten] | Unit | [ten] | 4.0 | Ten / Deca - Metric prefix = 10 - Dimensionless unit |
| [deca] | Unit | [deca] | 4.0 | Ten / Deca - Metric prefix = 10 - Dimensionless unit |
| [deci] | Unit | [deci] | 4.0 | Tenth / Deci - Metric prefix = 10⁻¹ - Dimensionless unit |
| [centi] | Unit | [centi] | 4.0 | Hundredth / Centi - Metric prefix = 10⁻² - Dimensionless unit |
| [milli] | Unit | [milli] | 4.0 | Thousandth / Milli - Metric prefix = 10⁻³ - Dimensionless unit |
| [mic] | Unit | [mic] | 4.0 | Millionth / Micro - Metric prefix = 10⁻⁶ - Dimensionless unit |
| [n] | Unit | [n] | 4.0 | Billionth / Nano - Metric prefix = 10⁻⁹ - Dimensionless unit |
| [p] | Unit | [p] | 4.0 | Trillionth / Pico - Metric prefix = 10⁻¹² - Dimensionless unit |
| [f] | Unit | [f] | 4.0 | Quadrillionth / Femto - Metric prefix = 10⁻¹⁵ - Dimensionless unit |
| [a] | Unit | [a] | 4.0 | Quintillionth / Atoo - Metric prefix = 10⁻¹⁸ - Dimensionless unit |
| [z] | Unit | [z] | 4.0 | Sextillionth / Zepto - Metric prefix = 10⁻²¹ - Dimensionless unit |
| [y] | Unit | [y] | 4.0 | Septillionth / Yocto - Metric prefix = 10⁻²⁴ - Dimensionless unit |
| Keyword | Type | Syntax | Since | Description |
|---|---|---|---|---|
| [m] | Unit | [m] | 4.0 | Meter - Unit of length [m] (m=1) - Unit |
| [km] | Unit | [km] | 4.0 | Kilometer - Unit of length [m] (m=1) - Unit |
| [cm] | Unit | [cm] | 4.0 | Centimeter - Unit of length [m] (m=1) - Unit |
| [mm] | Unit | [mm] | 4.0 | Millimeter - Unit of length [m] (m=1) - Unit |
| [inch] | Unit | [inch] | 4.0 | Inch - Unit of length [m] (m=1) - Unit |
| [yd] | Unit | [yd] | 4.0 | Yard - Unit of length [m] (m=1) - Unit |
| [ft] | Unit | [ft] | 4.0 | Feet - Unit of length [m] (m=1) - Unit |
| [mile] | Unit | [mile] | 4.0 | Mile - Unit of length [m] (m=1) - Unit |
| [nmi] | Unit | [nmi] | 4.0 | Nautical mile - Unit of length [m] (m=1) - Unit |
| Keyword | Type | Syntax | Since | Description |
|---|---|---|---|---|
| [m2] | Unit | [m2] | 4.0 | Square meter - Unit of area [m²] (m=1) - Unit |
| [cm2] | Unit | [cm2] | 4.0 | Square centimeter - Unit of area [m²] (m=1) - Unit |
| [mm2] | Unit | [mm2] | 4.0 | Square millimeter - Unit of area [m²] (m=1) - Unit |
| [are] | Unit | [are] | 4.0 | Are - Unit of area [m²] (m=1) - Unit |
| [ha] | Unit | [ha] | 4.0 | Hectare - Unit of area [m²] (m=1) - Unit |
| [acre] | Unit | [acre] | 4.0 | Acre - Unit of area [m²] (m=1) - Unit |
| [km2] | Unit | [km2] | 4.0 | Square kilometer - Unit of area [m²] (m=1) - Unit |
| Keyword | Type | Syntax | Since | Description |
|---|---|---|---|---|
| [mm3] | Unit | [mm3] | 4.0 | Cubic millimeter - Unit of volume [m³] (m=1) - Unit |
| [cm3] | Unit | [cm3] | 4.0 | Cubic centimeter - Unit of volume [m³] (m=1) - Unit |
| [m3] | Unit | [m3] | 4.0 | Cubic meter - Unit of volume [m³] (m=1) - Unit |
| [km3] | Unit | [km3] | 4.0 | Cubic kilometer - Unit of volume [m³] (m=1) - Unit |
| [ml] | Unit | [ml] | 4.0 | Milliliter - Unit of volume [m³] (m=1) - Unit |
| [l] | Unit | [l] | 4.0 | Liter - Unit of volume [m³] (m=1) - Unit |
| [gall] | Unit | [gall] | 4.0 | Gallon - Unit of volume [m³] (m=1) - Unit |
| [pint] | Unit | [pint] | 4.0 | Pint - Unit of volume [m³] (m=1) - Unit |
| Keyword | Type | Syntax | Since | Description |
|---|---|---|---|---|
| [s] | Unit | [s] | 4.0 | Second - Unit of time [s] (s=1) - Unit |
| [ms] | Unit | [ms] | 4.0 | Millisecond - Unit of time [s] (s=1) - Unit |
| [min] | Unit | [min] | 4.0 | Minute - Unit of time [s] (s=1) - Unit |
| [h] | Unit | [h] | 4.0 | Hour - Unit of time [s] (s=1) - Unit |
| [day] | Unit | [day] | 4.0 | Day - Unit of time [s] (s=1) - Unit |
| [week] | Unit | [week] | 4.0 | Week - Unit of time [s] (s=1) - Unit |
| [yearj] | Unit | [yearj] | 4.0 | Julian year = 365.25 days - Unit of time [s] (s=1) - Unit |
| Keyword | Type | Syntax | Since | Description |
|---|---|---|---|---|
| [kg] | Unit | [kg] | 4.0 | Kilogram - Unit of mass [kg] (kg=1) - Unit |
| [gr] | Unit | [gr] | 4.0 | Gram - Unit of mass [kg] (kg=1) - Unit |
| [mg] | Unit | [mg] | 4.0 | Milligram - Unit of mass [kg] (kg=1) - Unit |
| [dag] | Unit | [dag] | 4.0 | Decagram - Unit of mass [kg] (kg=1) - Unit |
| [t] | Unit | [t] | 4.0 | Tonne - Unit of mass [kg] (kg=1) - Unit |
| [oz] | Unit | [oz] | 4.0 | Ounce - Unit of mass [kg] (kg=1) - Unit |
| [lb] | Unit | [lb] | 4.0 | Pound - Unit of mass [kg] (kg=1) - Unit |
| Keyword | Type | Syntax | Since | Description |
|---|---|---|---|---|
| [b] | Unit | [b] | 4.0 | Bit - Unit of information [bit] (bit=1) - Unit |
| [kb] | Unit | [kb] | 4.0 | Kilobit - Unit of information [bit] (bit=1) - Unit |
| [Mb] | Unit | [Mb] | 4.0 | Megabit - Unit of information [bit] (bit=1) - Unit |
| [Gb] | Unit | [Gb] | 4.0 | Gigabit - Unit of information [bit] (bit=1) - Unit |
| [Tb] | Unit | [Tb] | 4.0 | Terabit - Unit of information [bit] (bit=1) - Unit |
| [Pb] | Unit | [Pb] | 4.0 | Petabit - Unit of information [bit] (bit=1) - Unit |
| [Eb] | Unit | [Eb] | 4.0 | Exabit - Unit of information [bit] (bit=1) - Unit |
| [Zb] | Unit | [Zb] | 4.0 | Zettabit - Unit of information [bit] (bit=1) - Unit |
| [Yb] | Unit | [Yb] | 4.0 | Yottabit - Unit of information [bit] (bit=1) - Unit |
| [B] | Unit | [B] | 4.0 | Byte - Unit of information [bit] (bit=1) - Unit |
| [kB] | Unit | [kB] | 4.0 | Kilobyte - Unit of information [bit] (bit=1) - Unit |
| [MB] | Unit | [MB] | 4.0 | Megabyte - Unit of information [bit] (bit=1) - Unit |
| [GB] | Unit | [GB] | 4.0 | Gigabyte - Unit of information [bit] (bit=1) - Unit |
| [TB] | Unit | [TB] | 4.0 | Terabyte - Unit of information [bit] (bit=1) - Unit |
| [PB] | Unit | [PB] | 4.0 | Petabyte - Unit of information [bit] (bit=1) - Unit |
| [EB] | Unit | [EB] | 4.0 | Exabyte - Unit of information [bit] (bit=1) - Unit |
| [ZB] | Unit | [ZB] | 4.0 | Zettabyte - Unit of information [bit] (bit=1) - Unit |
| [YB] | Unit | [YB] | 4.0 | Yottabyte - Unit of information [bit] (bit=1) - Unit |
| Keyword | Type | Syntax | Since | Description |
|---|---|---|---|---|
| [J] | Unit | [J] | 4.0 | Joule - Unit of energy [J] (m=1, kg=1, s=1) - Unit |
| [eV] | Unit | [eV] | 4.0 | Electronovolt - Unit of energy [J] (m=1, kg=1, s=1) - Unit |
| [keV] | Unit | [keV] | 4.0 | Kiloelectronovolt - Unit of energy [J] (m=1, kg=1, s=1) - Unit |
| [MeV] | Unit | [MeV] | 4.0 | Megaelectronovolt - Unit of energy [J] (m=1, kg=1, s=1) - Unit |
| [GeV] | Unit | [GeV] | 4.0 | Gigaelectronovolt - Unit of energy [J] (m=1, kg=1, s=1) - Unit |
| [TeV] | Unit | [TeV] | 4.0 | Teraelectronovolt - Unit of energy [J] (m=1, kg=1, s=1) - Unit |
| Keyword | Type | Syntax | Since | Description |
|---|---|---|---|---|
| [m/s] | Unit | [m/s] | 4.0 | Meter per second - Unit of speed [m/s] (m=1, s=1) - Unit |
| [km/h] | Unit | [km/h] | 4.0 | Kilometer per hour - Unit of speed [m/s] (m=1, s=1) - Unit |
| [mi/h] | Unit | [mi/h] | 4.0 | Mile per hour - Unit of speed [m/s] (m=1, s=1) - Unit |
| [knot] | Unit | [knot] | 4.0 | Knot - Unit of speed [m/s] (m=1, s=1) - Unit |
| Keyword | Type | Syntax | Since | Description |
|---|---|---|---|---|
| [m/s2] | Unit | [m/s2] | 4.0 | Meter per square second - Unit of acceleration [m/s²] (m=1, s=1) - Unit |
| [km/h2] | Unit | [km/h2] | 4.0 | Kilometer per square hour - Unit of acceleration [m/s²] (m=1, s=1) - Unit |
| [mi/h2] | Unit | [mi/h2] | 4.0 | Mile per square hour - Unit of acceleration [m/s²] (m=1, s=1) - Unit |
| Keyword | Type | Syntax | Since | Description |
|---|---|---|---|---|
| [rad] | Unit | [rad] | 4.0 | Radian - Unit of angle [rad] (rad=1) - Unit |
| [deg] | Unit | [deg] | 4.0 | Degree of arc - Unit of angle [rad] (rad=1) - Unit |
| ['] | Unit | ['] | 4.0 | Minute of arc - Unit of angle [rad] (rad=1) - Unit |
| [''] | Unit | [''] | 4.0 | Second of arc - Unit of angle [rad] (rad=1) - Unit |
| Keyword | Type | Syntax | Since | Description |
|---|---|---|---|---|
| ( | Parser symbol | ( ... ) | 1.0 | Left parentheses - Parser symbol |
| ) | Parser symbol | ( ... ) | 1.0 | Right parentheses - Parser symbol |
| , | Parser symbol | (a1, ... ,an) | 1.0 | Comma (function parameters) - Parser symbol |
| ; | Parser symbol | (a1; ... ;an) | 1.0 | Semicolon (function parameters) - Parser symbol |
| Parser symbol | 4.2 | Blank (whitespace) character - Parser symbol |
- please consider donation: DONATION
- or purchase the license via ORDER Page or INFIMA Online Store
Best regards, Mariusz Gromada