-
Notifications
You must be signed in to change notification settings - Fork 156
Commit
This commit does not belong to any branch on this repository, and may belong to a fork outside of the repository.
Merge pull request #1 from lightoj-dev/main
updating fork
- Loading branch information
Showing
16 changed files
with
1,606 additions
and
0 deletions.
There are no files selected for viewing
This file contains bidirectional Unicode text that may be interpreted or compiled differently than what appears below. To review, open the file in an editor that reveals hidden Unicode characters.
Learn more about bidirectional Unicode characters
| Original file line number | Diff line number | Diff line change |
|---|---|---|
| @@ -0,0 +1,52 @@ | ||
| # LOJ 1001 - Opposite Task | ||
|
|
||
| In this problem, you are given `T` test cases. Each test case contains an integer `n`, the value of which is `20` at max. Your task is to print out two non-negative integers `a` and `b`, such that `n = a + b`. Any values of `a` and `b` that satisfies the equation is accepted, however, neither of `a` nor `b` can be greater than `10`. | ||
|
|
||
| It is one of the easiest problems on LightOJ volumes. However, some people might find it difficult to get an `Accepted` verdict. The reason could be one of the following: | ||
| 1. Printing a number greater than 10 | ||
| 2. Failing to provide proper output format | ||
| 3. Missing new line on each line | ||
|
|
||
| If you are still stuck with this problem, check the codes below: | ||
|
|
||
| ### C | ||
| ----- | ||
| ```c | ||
| #include <stdio.h> | ||
| int main() { | ||
| int T, n; | ||
| scanf("%d", &T); | ||
| for (int i = 1; i <= T; i++) { | ||
| scanf("%d", &n); | ||
| if (n > 10) { | ||
| printf("10 %d\n", n - 10); | ||
| } else { | ||
| printf("0 %d\n", n); | ||
| } | ||
| } | ||
| return 0; | ||
| } | ||
| ``` | ||
|
|
||
| ### Java | ||
| ----- | ||
| ```java | ||
| package com.loj.volume; | ||
|
|
||
| import java.util.Scanner; | ||
|
|
||
| class OppositeTask { | ||
| public static void main(String[] args) throws Exception { | ||
| Scanner scanner = new Scanner(System.in); | ||
| int T = scanner.nextInt(), n; | ||
| for (int i = 1; i <= T; i++) { | ||
| n = scanner.nextInt(); | ||
| if (n > 10) { | ||
| System.out.printf("10 %d\n", n - 10); | ||
| } else { | ||
| System.out.printf("0 %d\n", n); | ||
| } | ||
| } | ||
| } | ||
| } | ||
| ``` |
This file contains bidirectional Unicode text that may be interpreted or compiled differently than what appears below. To review, open the file in an editor that reveals hidden Unicode characters.
Learn more about bidirectional Unicode characters
| Original file line number | Diff line number | Diff line change |
|---|---|---|
| @@ -0,0 +1,80 @@ | ||
| # LOJ 1007 - Mathematically Hard | ||
|
|
||
| _You have given `T` test cases and for each test case you have `a`, the lower bound, and `b`, the upper bound, find the summation of the | ||
| scores of the numbers from a to b (inclusive), where <br> | ||
| score (x) = n<sup>2</sup>,where n is the number of relatively prime numbers with x, which are smaller than x._ | ||
|
|
||
| --- | ||
|
|
||
| ### Summary | ||
|
|
||
| This is a number theory problem and for the `T` group of the input set, where each set consists of `a` and `b`, you have to find,square sum of all Euler function values from `a` to `b`. | ||
|
|
||
| ### Solution | ||
|
|
||
| Before you get to the solution let's have some idea about `Euler's totient function` aka `phi`.<br> | ||
|
|
||
| ``` | ||
| Euler's totient function, also known as phi-function `ϕ(n)`, counts the number of integers between `1` and `n` inclusive, which are `coprime` to `n`. Two numbers are coprime if their greatest common divisor equals `1` (`1` is considered to be coprime to any number). | ||
| ``` | ||
|
|
||
| Have a look: | ||
|
|
||
| - [wikipedia: Euler's totient function](https://en.wikipedia.org/wiki/Euler%27s_totient_function) | ||
| - [cp-algorithms: Euler's totient function](https://cp-algorithms.com/algebra/phi-function.html) | ||
|
|
||
| - [A quite useful cheat-sheet of CP: Phi Implementation](https://github.com/ar-pavel/CP-CheatSheet#631-euler-function) | ||
|
|
||
| Using Euler's totient function, calculate number of coprime for all the numbers until max possible input. Now, let's assume you have `phi[]` array that contains all the `ϕ(n)` values. As you will need to print the sum of square values of the `ϕ(n)`, loop through the `phi[]` array and multiply them with own value (`phi[i] = phi[i]*phi[i]`). Now your `phi[]` array contains square values of each `ϕ(n)`. For each query, as you need to print `sum(phi[a] ... phi[b])`, you can optimize this process by generating a [cumulative sum array](https://www.tutorialspoint.com/cplusplus-program-for-range-sum-queries-without-updates) of of `phi[]`. | ||
|
|
||
| The algorithm is: | ||
|
|
||
| - find all Phi values from `1 - rangeMax` | ||
| - calculate square value of each of them | ||
| - generate cumulative sum array of squared phi values | ||
| - for each query, print the `cumulative sum array[b]` - `cumulative sum array [a-1]` | ||
|
|
||
| ### C++ | ||
| ----- | ||
| ```cpp | ||
| #include <bits/stdc++.h> | ||
|
|
||
| using namespace std; | ||
|
|
||
| #define M 5000000 | ||
|
|
||
| int phi[M+2]; | ||
| unsigned long long phiSum[M+2]; | ||
|
|
||
| void calculatePhi(){ | ||
| for(int i=2; i<=M; i++) | ||
| phi[i] = i; | ||
| for(int i =2; i<=M; i++) | ||
| if(phi[i]==i) | ||
| for(int j=i; j<=M; j+=i) | ||
| phi[j]-=phi[j]/i; | ||
| } | ||
|
|
||
| int main(){ | ||
|
|
||
| calculatePhi(); | ||
| phiSum[1] = 0; | ||
|
|
||
| for(int i=2; i<=M; i++) | ||
| phiSum[i]= ((unsigned long long)phi[i]* (unsigned long long)phi[i])+phiSum[i-1]; | ||
|
|
||
| // for(int i=1; i<10; ++i) | ||
| // cout<<phi[i]<<" "<<phiSum[i]<<endl; | ||
| // deb(phi[2]); | ||
| // deb(phiSum[20]); | ||
|
|
||
| int tc,t(1); | ||
| for(scanf("%d",&tc); tc; ++t,--tc){ | ||
| int a,b; | ||
| scanf("%d%d",&a,&b); | ||
| unsigned long long x = phiSum[b]-phiSum[a-1]; | ||
| printf("Case %d: %llu\n",t,x); | ||
| } | ||
| return 0; | ||
| } | ||
| ``` |
This file contains bidirectional Unicode text that may be interpreted or compiled differently than what appears below. To review, open the file in an editor that reveals hidden Unicode characters.
Learn more about bidirectional Unicode characters
| Original file line number | Diff line number | Diff line change |
|---|---|---|
| @@ -0,0 +1,82 @@ | ||
| # 1014 - Ifter Party | ||
|
|
||
| _You have given `T` test cases and for each test case you have `P`, number of piaju in the beginning, and `L` piaju left end of the day, find the value `Q`, the number of piaju's each of `C` contestant ate._ | ||
|
|
||
| --- | ||
|
|
||
| ### Summary | ||
|
|
||
| This is a number theory problem and for the `T` group of the input set, where each set consists of `P` and `L` number, you have to find all the divisors of piaju's eaten or `(P-L)`. | ||
|
|
||
| ### Solution | ||
|
|
||
| Initially, you had `P` amount of piaju's, and end of the day it became `L`, so piaju's eaten by the contestants are `(P-L)`. As `C` contestants were invited and each of them ate `Q` piaju's each, `P - L = C * Q` stands true. So the result will be all possible divisors of `Q`, the number of piaju's each contestant ate. | ||
|
|
||
| The algorithm is: | ||
|
|
||
| - find the number of piaju's eaten | ||
| - find all the unique divisors of the 'count of eaten piaju's' | ||
| - sort and print all the divisors in ascending order that satisfy `(L<Q)` condition. | ||
| - if no such solution exists print `impossible`. | ||
|
|
||
| ### Code | ||
|
|
||
| #### C++ | ||
|
|
||
| ```cpp | ||
| #include <bits/stdc++.h> | ||
|
|
||
| using namespace std; | ||
|
|
||
| int main(){ | ||
| #ifndef ONLINE_JUDGE | ||
| freopen("in.txt","r",stdin); | ||
| freopen("out.txt","w",stdout); | ||
| #endif | ||
|
|
||
| int tc,t(1); | ||
| for(scanf("%d",&tc); tc; ++t,--tc){ | ||
| long long piaju,left; | ||
|
|
||
| scanf("%lld%lld", &piaju,&left); | ||
|
|
||
| // exception | ||
| if(left*2>=piaju){ | ||
| printf("Case %d: impossible\n",t); | ||
| continue; | ||
| } | ||
|
|
||
| printf("Case %d:",t); | ||
|
|
||
|
|
||
| long long piajuEaten = piaju-left; | ||
| // cout<<piajuEaten<<endl; | ||
|
|
||
| vector<long long> possibleValueOfQ; | ||
|
|
||
|
|
||
| // find all the divisors of piajuEaten | ||
| for(long long i=1; i*i<=piajuEaten; ++i) | ||
| if(piajuEaten%i==0){ | ||
| possibleValueOfQ.push_back(i); | ||
|
|
||
| if(piaju/i!=i) | ||
| possibleValueOfQ.push_back(piajuEaten/i); | ||
| } | ||
|
|
||
| // sort the divisors to print the answer in ascending order | ||
| sort(possibleValueOfQ.begin(), possibleValueOfQ.end()); | ||
|
|
||
| // print the divisors | ||
| for(auto x: possibleValueOfQ) | ||
| // if(x>left) | ||
| printf(" %lld",x); | ||
|
|
||
|
|
||
| printf("\n"); | ||
| } | ||
|
|
||
| return 0; | ||
| } | ||
|
|
||
| ``` |
This file contains bidirectional Unicode text that may be interpreted or compiled differently than what appears below. To review, open the file in an editor that reveals hidden Unicode characters.
Learn more about bidirectional Unicode characters
| Original file line number | Diff line number | Diff line change |
|---|---|---|
| @@ -0,0 +1,146 @@ | ||
| # LOJ 1029 - Civil and Evil Engineer | ||
|
|
||
| ### Problem Summary | ||
|
|
||
| You have `n` houses `[1-n]` and a power station `0`. You are also given a set of wires, where every wire is in `u v w` format, meaning `connection from u to v costs w`. You have to use exactly `n` wires from the set to connect the houses with the power station. **The connections can be direct or indirect (through some houses) but there must be a path of wires from every house to the power station.** | ||
|
|
||
| ### Observations | ||
|
|
||
| We can see the following properties in the problem structure. | ||
|
|
||
| - **Graph**: We can consider the houses and the power station as `nodes` in a graph, and the wires as `edges`. Since the costs of connecting two nodes are given, and the connections have no direction, so this is a `Weighted Undirected Graph`. | ||
|
|
||
| - **Tree**: In total, we have `n+1` nodes (`n` houses and `1` power station). We have to connect them using exactly `n` wires or `edges`. We know in a tree, for `N` nodes we have `N-1` edges. So the problem is asking us to convert the graph into a tree. | ||
|
|
||
| - **Minimum Spanning Tree**: For the `best possible connection scheme`, We have to connect all houses with the power station using minimum cost. We have to pick `edges` in a way that satisfies the cost minimization. Therefore, we have to compute the `Minimum Spanning Tree` of the graph. | ||
|
|
||
| - `Minimum Spanning Tree` of a graph is a subtree of that graph that contains all the `nodes` and the `sum of edge weights` is minimum possible. You can use [Prim's algorithm](https://cp-algorithms.com/graph/mst_prim.html) or [Kruskal's Algorithm](https://cp-algorithms.com/graph/mst_kruskal.html) to implement the Minimum Spanning Tree. | ||
|
|
||
| - **Maximum Spanning Tree**: We also have to calculate the maximum possible cost to connect all the `nodes`, since this is the `worst possible connection scheme`. For this, we have to pick `edges` in a way that maximizes the cost. So we also have to compute the `Maximum Spanning Tree` of the graph. | ||
| - `Maximum Spanning Tree` of a graph is a subtree of that graph that contains all the `nodes` and the `sum of edge weights` is maximum possible. We can tweak the Minimum Spanning Tree algorithm (sort the edges in descending order of the weights) to implement Maximum Spanning Tree. | ||
|
|
||
| ### Solution | ||
|
|
||
| For every case, we have to calculate minimum spanning tree `cost1` and maximum spanning tree `cost2` and then average their costs, thus `(cost1 + cost2) / 2`. If `(cost1 + cost2)` is not divisible by `2` then we have to print in `p/q` format. Where `p` is `(cost1 + cost2)` and `q` is `2`. For example, `229/2`. | ||
|
|
||
| ### Simulation | ||
|
|
||
| Simulation of **test case 2** is given below. | ||
|
|
||
| 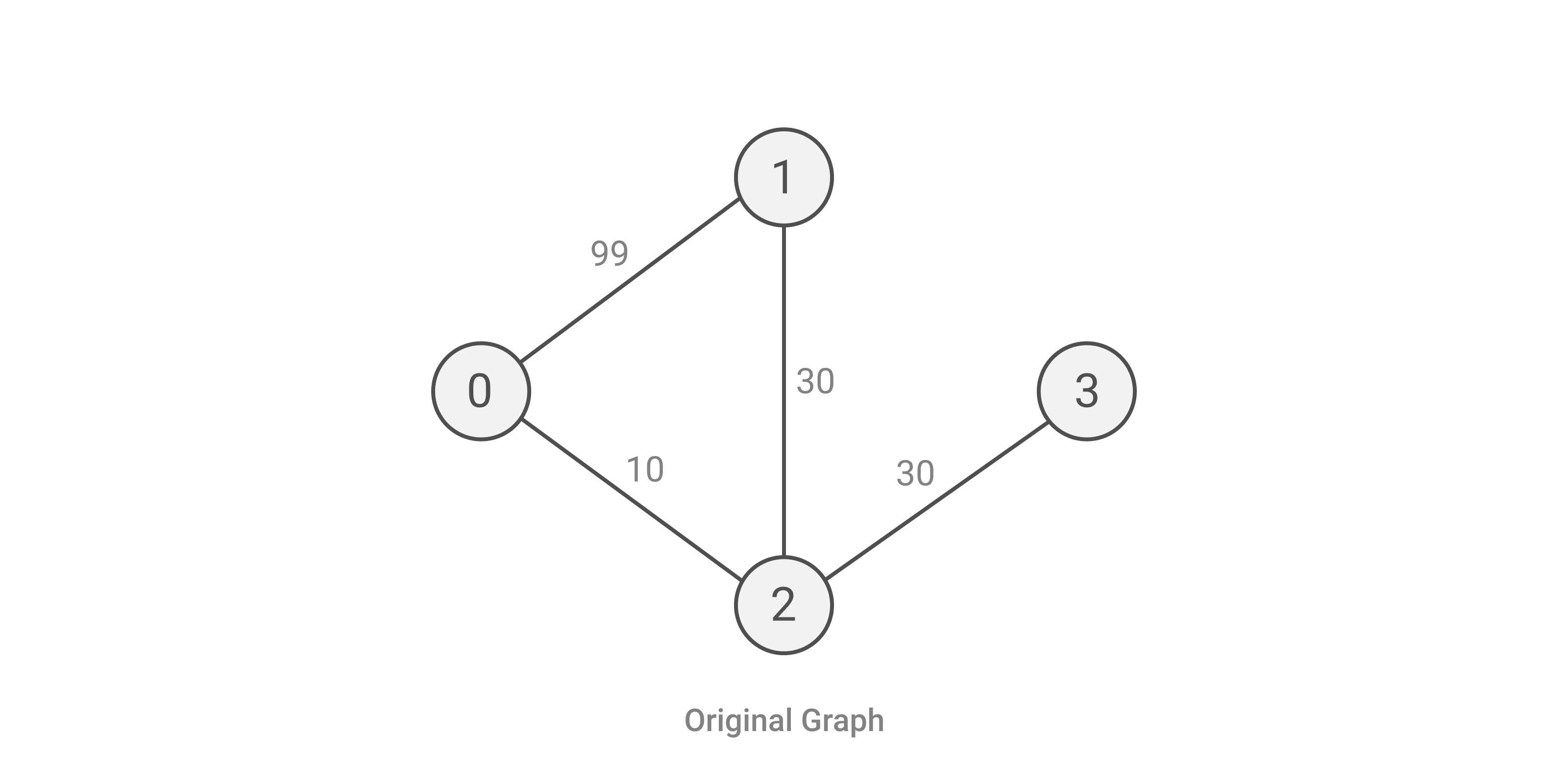 | ||
|
|
||
| 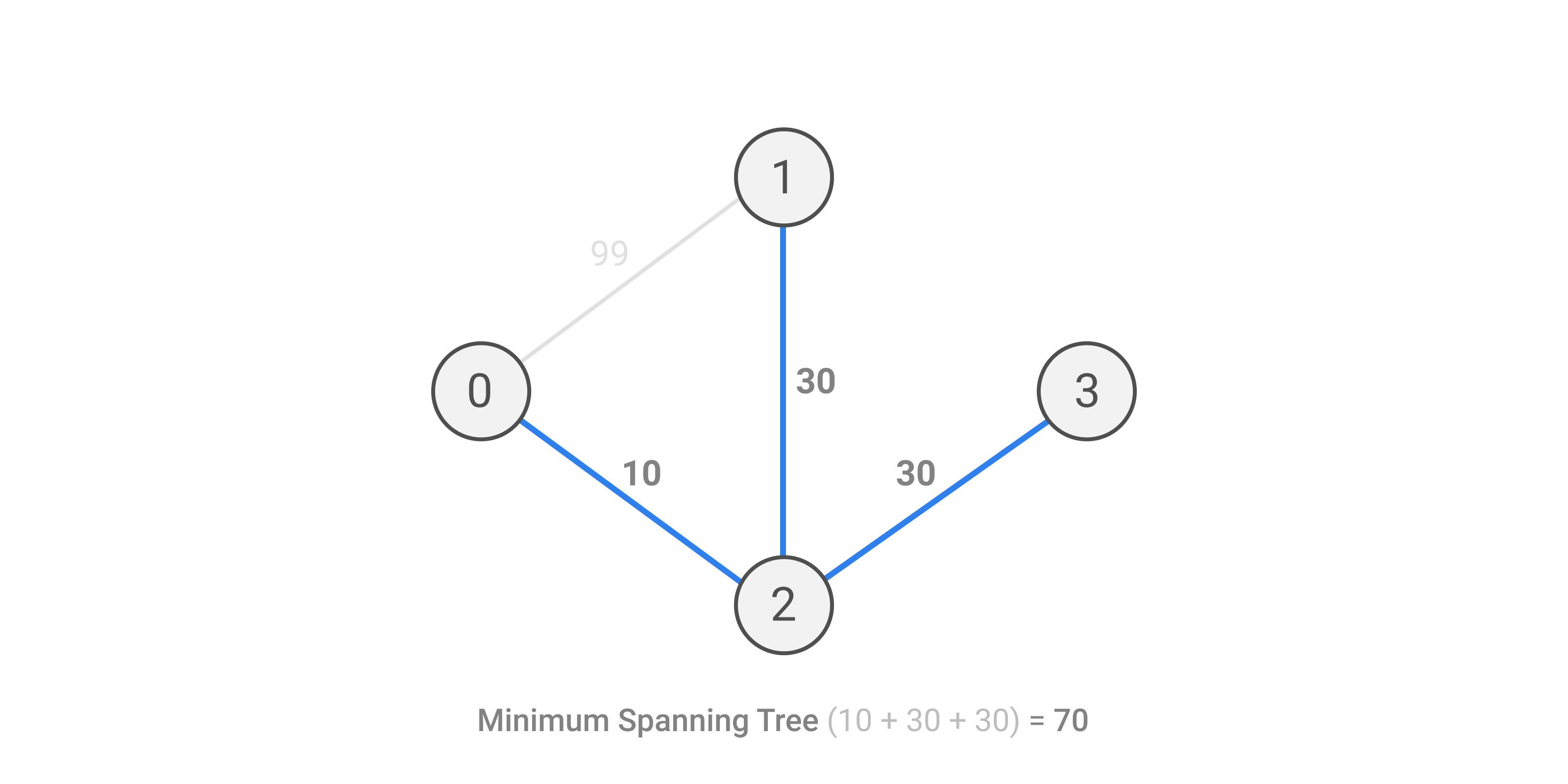 | ||
|
|
||
| 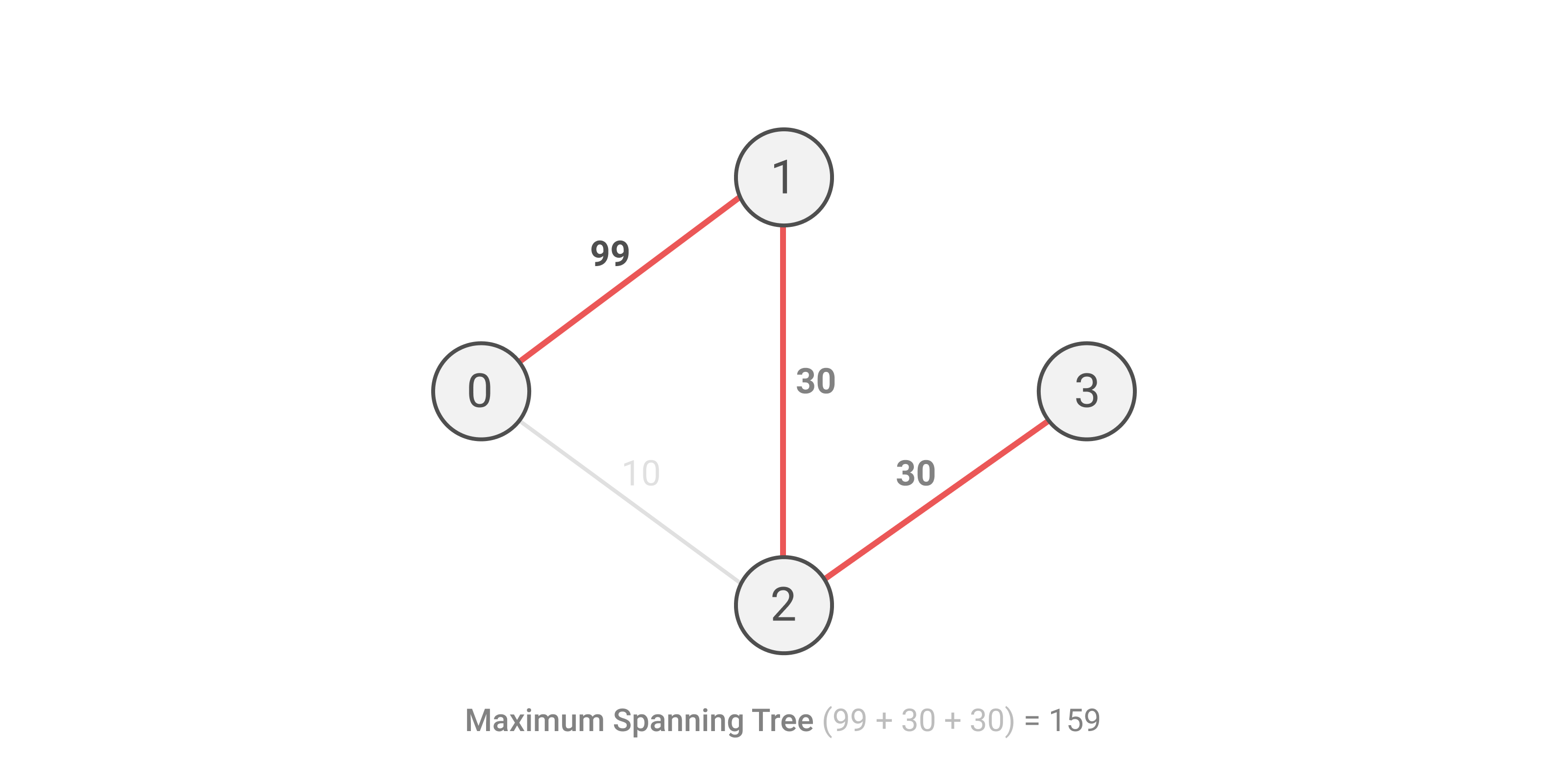 | ||
|
|
||
| And the answer is `(70 + 159) / 2`. Since `229` is not divisible by `2`, we print `229/2`. | ||
|
|
||
| ### C++ | ||
|
|
||
| --- | ||
|
|
||
| ```C++ | ||
| #include<bits/stdc++.h> | ||
| using namespace std; | ||
|
|
||
| struct edge{ | ||
| int u, v, w; | ||
| }; | ||
|
|
||
| bool cmp(edge A, edge B){ | ||
| return A.w < B.w; | ||
| } | ||
|
|
||
| // edge list | ||
| vector < edge > G; | ||
|
|
||
| int n; // total nodes | ||
| int parent[105]; | ||
|
|
||
| // function to clear graph | ||
| void _init(){ | ||
| G.clear(); | ||
| } | ||
|
|
||
| // function to find parent of a disjoint set | ||
| int Find(int u){ | ||
| if (u==parent[u]) return u; | ||
| return parent[u] = Find(parent[u]); | ||
| } | ||
|
|
||
| // Kruskal's algorithm with Disjoint-Set Union method is used | ||
| // minimum spanning tree | ||
| long long MinST(){ | ||
| // reset parent table [0-n] | ||
| for (int i = 0; i <= n; i++) | ||
| parent[i] = i; | ||
|
|
||
| long long cost = 0; | ||
| // forward iteration for minimum cost first | ||
| for (int i = 0; i < G.size(); i++){ | ||
| int u = G[i].u; | ||
| int v = G[i].v; | ||
| int w = G[i].w; | ||
|
|
||
| int p = Find(u); | ||
| int q = Find(v); | ||
| if (p!=q){ | ||
| cost += w; | ||
| parent[q] = p; | ||
| } | ||
| } | ||
| return cost; | ||
| } | ||
|
|
||
| // maximum spanning tree | ||
| long long MaxST(){ | ||
| // reset parent table [0-n] | ||
| for (int i = 0; i <= n; i++) | ||
| parent[i] = i; | ||
|
|
||
| long long cost = 0; | ||
| // backward iteration for maximum cost first | ||
| for (int i = G.size()-1; i >= 0; i--){ | ||
| int u = G[i].u; | ||
| int v = G[i].v; | ||
| int w = G[i].w; | ||
|
|
||
| int p = Find(u); | ||
| int q = Find(v); | ||
| if (p!=q){ | ||
| cost += w; | ||
| parent[q] = p; | ||
| } | ||
| } | ||
| return cost; | ||
| } | ||
|
|
||
| int main() | ||
| { | ||
| int T; scanf("%d", &T); | ||
| for (int cs = 1; cs <= T; cs++){ | ||
| _init(); // reset graph | ||
|
|
||
| scanf("%d", &n); | ||
| int u, v, w; | ||
|
|
||
| // take input until all u, v, w are zero (0) | ||
| while ( scanf("%d%d%d", &u, &v, &w) && (u!=0 || v!=0 || w!=0) ){ | ||
| G.push_back({u, v, w}); | ||
| } | ||
|
|
||
| // sorting is only done once | ||
| // forward and backward iterations will be done | ||
| // for ascending and descending order traversal | ||
| sort(G.begin(), G.end(), cmp); | ||
|
|
||
| long long cost1 = MinST(); | ||
| long long cost2 = MaxST(); | ||
|
|
||
| long long cost = cost1 + cost2; | ||
| if (cost%2 == 0) printf("Case %d: %lld\n", cs, cost/2); | ||
| else printf("Case %d: %lld/2\n", cs, cost); // cost/2 format | ||
| } | ||
| return 0; | ||
| } | ||
| ``` |
Loading
Sorry, something went wrong. Reload?
Sorry, we cannot display this file.
Sorry, this file is invalid so it cannot be displayed.
Loading
Sorry, something went wrong. Reload?
Sorry, we cannot display this file.
Sorry, this file is invalid so it cannot be displayed.
Loading
Sorry, something went wrong. Reload?
Sorry, we cannot display this file.
Sorry, this file is invalid so it cannot be displayed.
Oops, something went wrong.