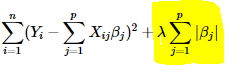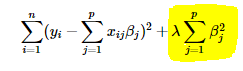2. Machine Learning Techniques
Multiple Linear Regression is a statistical technique which forms the basis for many advanced ML techniques. Multiple Regression predicts the value of the target variable based on a linear combination of input variables with respective weights. Weights for each input variables are learned by minimizing a loss function. We used squared error as loss function based on its efficacy.
Lasso Regression is a type of Multiple Linear regression with an L1 regularization penalty on weights. Lasso also performs feature selection on its own due to L1 penalty which can reduce weights to zero if a feature is not useful to overall model performance. A regularization parameter, lambda decides the magnitude of the impact of regularization.
Similarly, Ridge Regression is also a type of Multiple Linear regression with an L2 regularization penalty on its weights. Unlike Lasso, Ridge does not perform feature selection.
Elastic net combines both L1 and L2 norm with a parameter p and 1-p, where p< 1.
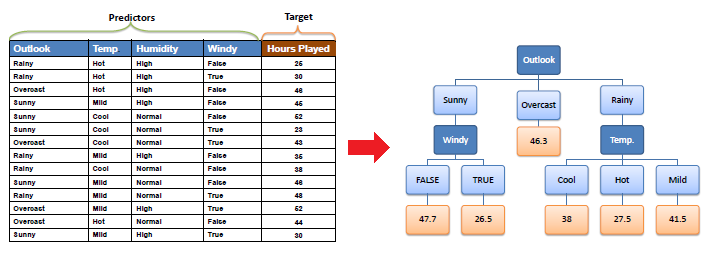
Decision tree builds regression models in the form of a tree structure. It breaks down a dataset into smaller and smaller subsets. The final result is a tree with decision nodes and leaf nodes. A decision node has two or more branches, each representing values for the attribute tested. Leaf node represents a decision on the numerical target.
Random Forest Regression is an ensemble of Decision trees, which greatly reduces the risk of overfitting. Generally, the ensemble method used is Bootstrap Aggregating. M subsamples of training instances are created from N training instances with replacement, and models are built on each subsample. And the output is taken as average.
It employs Boosting ensemble method to decision trees, where each subsequent predictor learns from the mistakes of the previous one. Usually, it’s done by overly representing error terms. In Gradient Boosting, the same general idea is employed by Gradients of loss functions, where each subsequent predictor changes based on loss of the previous one.