Triangulation of polygon

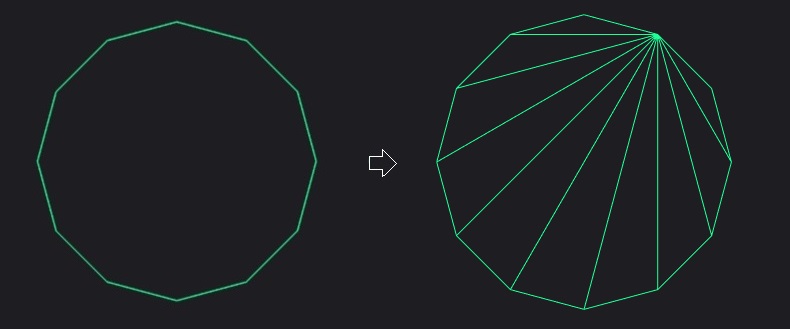
This algorithm can triangulate both convex and concave 3D polygons that lie in the same 3D plane.

Triangulation of a polygon is the process of dividing a polygon into a series of triangles.

Triangulate a obj file

pyTriangulate have been integrated into the pyOBJTriangulate, showcasing the triangulation capabilities.

Example Convex polygon

A convex polygon is a polygon with the following characteristics:

• All interior angles are less than 180 degrees.
• Any line segment drawn between two points inside the polygon will always remain entirely inside the polygon.

import Triangulate

polygon = [
    Triangulate.Point(0.5, 0.866, 0.0),     #  1 o'clock
    Triangulate.Point(0.866, 0.5, 0.0),     #  2 o'clock
    Triangulate.Point(1.0, 0.0, 0.0),       #  3 o'clock
    Triangulate.Point(0.866, -0.5, 0.0),    #  4 o'clock
    Triangulate.Point(0.5, -0.866, 0.0),    #  5 o'clock
    Triangulate.Point(0.0, -1.0, 0.0),      #  6 o'clock
    Triangulate.Point(-0.5, -0.866, 0.0),   #  7 o'clock
    Triangulate.Point(-0.866, -0.5, 0.0),   #  8 o'clock
    Triangulate.Point(-1.0, 0.0, 0.0),      #  9 o'clock
    Triangulate.Point(-0.866, 0.5, 0.0),    # 10 o'clock
    Triangulate.Point(-0.5, 0.866, 0.0),    # 11 o'clock
    Triangulate.Point(0.0, 1.0, 0.0)        # 12 o'clock
]

# Convert polygon to triangles
triangles, normal = Triangulate.triangulate(polygon)

When triangulating the polygon, the initial step involves identifying the polygon's nature. If the polygon proves to be convex, the routine will proceed with triangulation using the fan algorithm. The fan algorithm is a common and efficient method for triangulating convex polygons.

Example Concave polygon

A concave polygon is a polygon with the following characteristics:

• At least one of its interior angles measures more than 180 degrees. This means that there is at least one corner (vertex) in the polygon where the shape appears to bend inwards or "fold" in a way that creates an angle greater than 180 degrees.
• Unlike convex polygons, in a concave polygon, you can draw a line segment between two points inside the polygon that may extend outside the boundaries of the polygon. This happens because of the "inward" or "folded" angles within the polygon.

import Triangulate

polygon = [
    Triangulate.Point(0.5, 0.866, 0.0),     #  1 o'clock
    Triangulate.Point(0.866, 0.5, 0.0),     #  2 o'clock
    Triangulate.Point(0.0, 1.0, 0.0)        #  center clock
    Triangulate.Point(0.866, -0.5, 0.0),    #  4 o'clock
    Triangulate.Point(0.5, -0.866, 0.0),    #  5 o'clock
    Triangulate.Point(0.0, -1.0, 0.0),      #  6 o'clock
    Triangulate.Point(-0.5, -0.866, 0.0),   #  7 o'clock
    Triangulate.Point(-0.866, -0.5, 0.0),   #  8 o'clock
    Triangulate.Point(-1.0, 0.0, 0.0),      #  9 o'clock
    Triangulate.Point(-0.866, 0.5, 0.0),    # 10 o'clock
    Triangulate.Point(-0.5, 0.866, 0.0),    # 11 o'clock
    Triangulate.Point(0.0, 1.0, 0.0)        # 12 o'clock
]

# Convert polygon to triangles
triangles, normal = Triangulate.triangulate(polygon)

If the polygon proves to be concave, the routine will proceed with triangulation using the ear-clipping algorithm.