Home
Accessibility in spatial applications is the quality of how easy it is to reach (a) destination location(s).
It is an important driving factor in Land Use Modelling and also relevant for many other applications.
- How to find the shortest path between an origin and destination
- Network optimisation algorithms
- What if you want to look at more than one origin and or destination
- How can we use these matrices to say something about accessibility (diving into Spatial Interaction Models)
- Overview of useful Accessibility indicators
- Applications
The shortest path that has to be found does not necessarily need to be about minimising distance, but it could also be travel time, travel cost, or any metric you could think of. A more general way to think about this is to minimise the impedance of a segment (e.g., a piece of road) in the network. The procedure for finding the shortest path is a large part of graph theory.
The dijkstra algorithm determines the minimum impedance of the routes through a network/graph of nodes and links with given link-impedance for each combination of given origins and destinations.
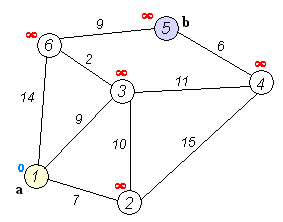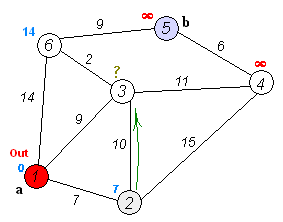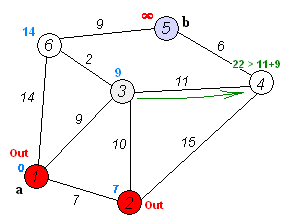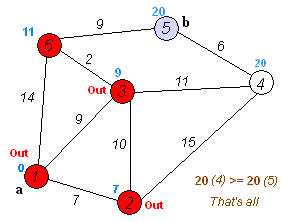
---- explain in more detail how it works
- make sure links are not doubled (i.e. with a return trip), and if necessary reverse the start and end nodes.
- transform link set from arcs to segments (i.e. links with only two nodes).
- remove dead ends in the network (if a node has only one link)
- remove nodes from a junction-free section, and aggregate relevant data field (original link length and impedance)
- repeat removing dead-end and junction-free sections until no more nodes are removed.
See here for a detailed description of the algorithm
Finding the path with the lowest impedance from A to B is relatively easy with Dijkstra's algorithm. However, for many applications, it is very useful to calculate this for a large set of origins and/or destinations.
The following text is based on and citated from De Vries, Nijkamp & Rietveld (2000).
- travel time to reach x amount of people
- how many people can be reached within x minutes of travel
- average travel time to all populated cells within 120km Euclidean and within 4 hours
- potential accessibility to destination population with a distance decay function
- EU networks
- Public transport modelling
An important distinction needs to be made between:
- impedances in a Euclidean space (as the crow flies)
- impedances over a network
With the GeoDMS both types of impedances can be calculated, but usually, networks are used to calculate more realistic impedances. The GeoDMS contains network functions to build a network topology and use it in impedance functions to calculate impedances per origin point or in an origin/destination matrix (trip table).
Much attention has been given to making network calculations fast and efficient. This allows users to calculate impedances in large networks in a limited time.
- Accessibility measures are calculated and used as driving factors for Land Use Modelling
- Origin Destination matrix (trip table) for many applications
- In our projects in the social domain, distances from houses to services are calculated. These distances are important suitability factors for housing for persons with mobility issues.
