问题描述
Tromino是一个由棋盘上的三个邻接方块组成的L型瓦片。我们的问题是,如何用Tromino覆盖一个缺少了一个方块(可以在棋盘上的任何位置)的$2^n*2^n$棋盘。除了这个缺失的方块,Tromino应该覆盖棋盘上的所有方块,而且不能有重叠。
目标
用分治法的思想设计一个解决Tromino谜题的算法,用JavaScript实现算法,并用html+css编写页面展示算法效果
问题分析
题目要求用分治法来解决该问题。该问题中缺失方块的位置是任意的,棋盘大小是2的n次方(n为正整数)的矩阵。
我们先来考虑最小规模即当n=1时的情况。这种情况下无论缺失的方块在哪个位置,我们只需要将剩下的三个方块填充就好,相当于放置一个骨牌。
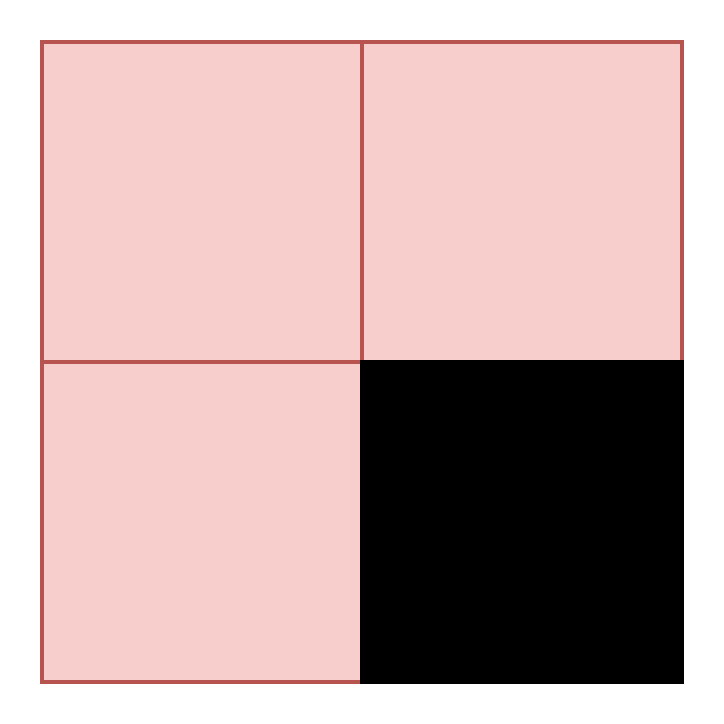
当n=2时,方块数为4*4,划分子问题前,我们先将棋盘分为四个象限,确定缺失方块的象限后,将其它三个象限距离中心位置最近的一个方块填充。
此时我们再将其划分为四个方块数为2*2的矩阵,将已经填充的方块看作缺失方块,则每个小规模矩阵都有一个缺失方块,即它们是规模相同的子问题,依次递归最后将整个棋盘填充完整。
算法描述
定义函数run(centerX,centerY,loseX,loseY,len),centerX/centerY是中点位置,loseX/loseY是确实点位置,len是格子长度。
如果:loseX < centerX && loseY < centerY,即缺失方块在左上方,如果要填充左下放的格子,那么centerX/centerY需要增加len/4,并将中心点左下的格子设为缺失点,再次调用run()方法。其他方向也类似
最后的终止条件是len < 2
难点
递归的参数如何变化