0662. 二叉树最大宽度.md

0662. 二叉树最大宽度

• 标签：树、深度优先搜索、广度优先搜索、二叉树
• 难度：中等

题目链接

• 0662. 二叉树最大宽度 - 力扣

题目大意

描述：给你一棵二叉树的根节点 root。

要求：返回树的最大宽度。

说明：

• 每一层的宽度：为该层最左和最右的非空节点（即两个端点）之间的长度。将这个二叉树视作与满二叉树结构相同，两端点间会出现一些延伸到这一层的 null 节点，这些 null 节点也计入长度。
• 树的最大宽度：是所有层中最大的宽度。
• 题目数据保证答案将会在 32 位带符号整数范围内。
• 树中节点的数目范围是 $[1, 3000]$。
• $-100 \le Node.val \le 100$。

示例：

• 示例 1：

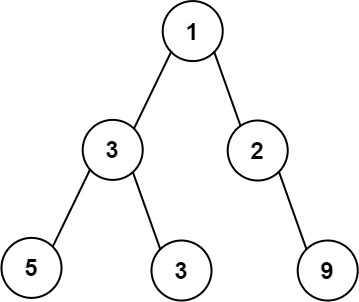
输入：root = [1,3,2,5,3,null,9]
输出：4
解释：最大宽度出现在树的第 3 层，宽度为 4 (5,3,null,9)。

• 示例 2：

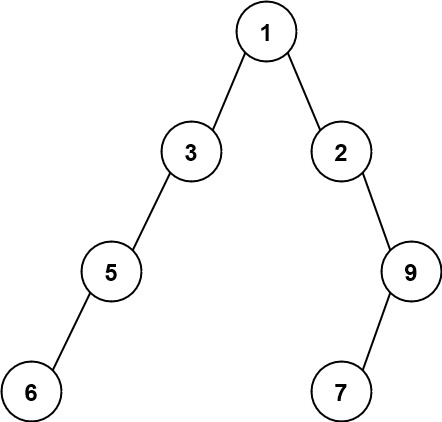
输入：root = [1,3,2,5,null,null,9,6,null,7]
输出：7
解释：最大宽度出现在树的第 4 层，宽度为 7 (6,null,null,null,null,null,7) 。

解题思路

思路 1：广度优先搜索

最直观的做法是，求出每一层的宽度，然后求出所有层高度的最大值。

在计算每一层宽度时，根据题意，两端点之间的 null 节点也计入长度，所以我们可以对包括 null 节点在内的该二叉树的所有节点进行编号。

也就是满二叉树的编号规则：如果当前节点的编号为 $i$，则左子节点编号记为 $i \times 2 + 1$，则右子节点编号为 $i \times 2 + 2$。

接下来我们使用广度优先搜索方法遍历每一层的节点，在向队列中添加节点时，将该节点与该节点对应的编号一同存入队列中。

这样在计算每一层节点的宽度时，我们可以通过队列中队尾节点的编号与队头节点的编号，快速计算出当前层的宽度。并计算出所有层宽度的最大值。

思路 1：代码

class Solution:
    def widthOfBinaryTree(self, root: Optional[TreeNode]) -> int:
        if not root:
            return False

        queue = collections.deque([[root, 0]])
        ans = 0
        while queue:
            ans = max(ans, queue[-1][1] - queue[0][1] + 1)
            size = len(queue)
            for _ in range(size):
                cur, index = queue.popleft()
                if cur.left:
                    queue.append([cur.left, index * 2 + 1])
                if cur.right:
                    queue.append([cur.right, index * 2 + 2])
        return ans

思路 1：复杂度分析

• 时间复杂度：$O(n)$，其中 $n$ 为二叉树的节点数。
• 空间复杂度：$O(n)$。