- 标签:位运算、数组、回溯
- 难度:中等
描述:给定一个整数数组 nums,数组中的元素互不相同。
要求:返回该数组所有可能的不重复子集。可以按任意顺序返回解集。
说明:
-
$1 \le nums.length \le 10$ 。 -
$-10 \le nums[i] \le 10$ 。 -
nums中的所有元素互不相同。
示例:
- 示例 1:
输入 nums = [1,2,3]
输出 [[],[1],[2],[1,2],[3],[1,3],[2,3],[1,2,3]]- 示例 2:
输入:nums = [0]
输出:[[],[0]]数组的每个元素都有两个选择:选与不选。
我们可以通过向当前子集数组中添加可选元素来表示选择该元素。也可以在当前递归结束之后,将之前添加的元素从当前子集数组中移除(也就是回溯)来表示不选择该元素。
下面我们根据回溯算法三步走,写出对应的回溯算法。
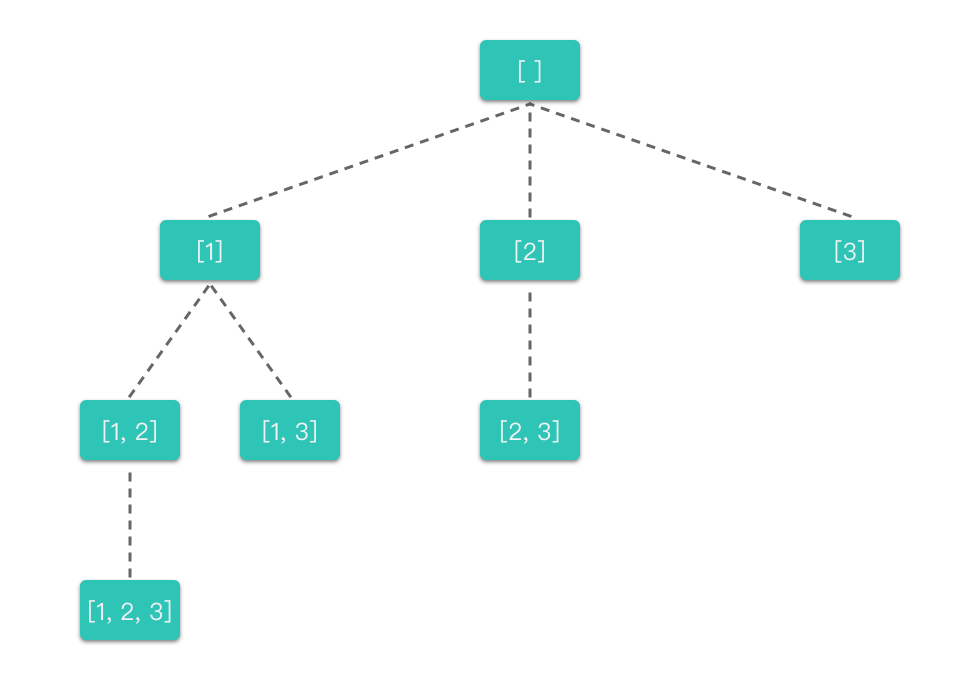
- 明确所有选择:根据数组中每个位置上的元素选与不选两种选择,画出决策树,如下图所示。
-
明确终止条件:
- 当遍历到决策树的叶子节点时,就终止了。即当前路径搜索到末尾时,递归终止。
-
将决策树和终止条件翻译成代码:
-
定义回溯函数:
backtracking(nums, index):函数的传入参数是nums(可选数组列表)和index(代表当前正在考虑元素是nums[i]),全局变量是res(存放所有符合条件结果的集合数组)和path(存放当前符合条件的结果)。backtracking(nums, index):函数代表的含义是:在选择nums[index]的情况下,递归选择剩下的元素。
-
书写回溯函数主体(给出选择元素、递归搜索、撤销选择部分)。
- 从当前正在考虑元素,到数组结束为止,枚举出所有可选的元素。对于每一个可选元素:
- 约束条件:之前选过的元素不再重复选用。每次从
index位置开始遍历而不是从0位置开始遍历就是为了避免重复。集合跟全排列不一样,子集中{1, 2}和{2, 1}是等价的。为了避免重复,我们之前考虑过的元素,就不再重复考虑了。 - 选择元素:将其添加到当前子集数组
path中。 - 递归搜索:在选择该元素的情况下,继续递归考虑下一个位置上的元素。
- 撤销选择:将该元素从当前子集数组
path中移除。
- 约束条件:之前选过的元素不再重复选用。每次从
- 从当前正在考虑元素,到数组结束为止,枚举出所有可选的元素。对于每一个可选元素:
for i in range(index, len(nums)): # 枚举可选元素列表 path.append(nums[i]) # 选择元素 backtracking(nums, i + 1) # 递归搜索 path.pop() # 撤销选择
- 明确递归终止条件(给出递归终止条件,以及递归终止时的处理方法)。
- 当遍历到决策树的叶子节点时,就终止了。也就是当正在考虑的元素位置到达数组末尾(即
start >= len(nums))时,递归停止。 - 从决策树中也可以看出,子集需要存储的答案集合应该包含决策树上所有的节点,应该需要保存递归搜索的所有状态。所以无论是否达到终止条件,我们都应该将当前符合条件的结果放入到集合中。
- 当遍历到决策树的叶子节点时,就终止了。也就是当正在考虑的元素位置到达数组末尾(即
-
class Solution:
def subsets(self, nums: List[int]) -> List[List[int]]:
res = [] # 存放所有符合条件结果的集合
path = [] # 存放当前符合条件的结果
def backtracking(nums, index): # 正在考虑可选元素列表中第 index 个元素
res.append(path[:]) # 将当前符合条件的结果放入集合中
if index >= len(nums): # 遇到终止条件(本题)
return
for i in range(index, len(nums)): # 枚举可选元素列表
path.append(nums[i]) # 选择元素
backtracking(nums, i + 1) # 递归搜索
path.pop() # 撤销选择
backtracking(nums, 0)
return res-
时间复杂度:$O(n \times 2^n)$,其中
$n$ 指的是数组nums的元素个数,$2^n$ 指的是所有状态数。每种状态需要$O(n)$ 的时间来构造子集。 -
空间复杂度:$O(n)$,每种状态下构造子集需要使用
$O(n)$ 的空间。
对于一个元素个数为 n 的集合 nums 来说,每一个位置上的元素都有选取和未选取两种状态。我们可以用数字 1 来表示选取该元素,用数字 0 来表示不选取该元素。
那么我们就可以用一个长度为 n 的二进制数来表示集合 nums 或者表示 nums 的子集。其中二进制的每一位数都对应了集合中某一个元素的选取状态。对于集合中第 i 个元素(i 从 0 开始编号)来说,二进制对应位置上的 1 代表该元素被选取,0 代表该元素未被选取。
举个例子来说明一下,比如长度为 5 的集合 nums = {5, 4, 3, 2, 1},我们可以用一个长度为 5 的二进制数来表示该集合。
比如二进制数 11111 就表示选取集合的第 0 位、第 1 位、第 2 位、第 3 位、第 4 位元素,也就是集合 {5, 4, 3, 2, 1} ,即集合 nums 本身。如下表所示:
| 集合 nums 对应位置(下标) | 4 | 3 | 2 | 1 | 0 |
|---|---|---|---|---|---|
| 二进制数对应位数 | 1 | 1 | 1 | 1 | 1 |
| 对应选取状态 | 选取 | 选取 | 选取 | 选取 | 选取 |
再比如二进制数 10101 就表示选取集合的第 0 位、第 2 位、第 5 位元素,也就是集合 {5, 3, 1}。如下表所示:
| 集合 nums 对应位置(下标) | 4 | 3 | 2 | 1 | 0 |
|---|---|---|---|---|---|
| 二进制数对应位数 | 1 | 0 | 1 | 0 | 1 |
| 对应选取状态 | 选取 | 未选取 | 选取 | 未选取 | 选取 |
再比如二进制数 01001 就表示选取集合的第 0 位、第 3 位元素,也就是集合 {5, 2}。如下标所示:
| 集合 nums 对应位置(下标) | 4 | 3 | 2 | 1 | 0 |
|---|---|---|---|---|---|
| 二进制数对应位数 | 0 | 1 | 0 | 0 | 1 |
| 对应选取状态 | 未选取 | 选取 | 未选取 | 未选取 | 选取 |
通过上面的例子我们可以得到启发:对于长度为 5 的集合 nums 来说,我们只需要从 00000 ~ 11111 枚举一次(对应十进制为 5 的集合 S 的所有子集。
我们将上面的例子拓展到长度为 n 的集合 nums。可以总结为:
- 对于长度为
5的集合nums来说,只需要枚举$0 \sim 2^n - 1$ (共$2^n$ 种情况),即可得到所有的子集。
class Solution:
def subsets(self, nums: List[int]) -> List[List[int]]:
n = len(nums) # n 为集合 nums 的元素个数
sub_sets = [] # sub_sets 用于保存所有子集
for i in range(1 << n): # 枚举 0 ~ 2^n - 1
sub_set = [] # sub_set 用于保存当前子集
for j in range(n): # 枚举第 i 位元素
if i >> j & 1: # 如果第 i 为元素对应二进制位为 1,则表示选取该元素
sub_set.append(nums[j]) # 将选取的元素加入到子集 sub_set 中
sub_sets.append(sub_set) # 将子集 sub_set 加入到所有子集数组 sub_sets 中
return sub_sets # 返回所有子集-
时间复杂度:$O(n \times 2^n)$,其中
$n$ 指的是数组nums的元素个数,$2^n$ 指的是所有状态数。每种状态需要$O(n)$ 的时间来构造子集。 -
空间复杂度:$O(n)$,每种状态下构造子集需要使用
$O(n)$ 的空间。