三维坐标中两个向量的叉乘(Cross Product),也称为向量积,结果是一个向量而非标量。给定两个向量 (
如果 ($\vec{a} = (a_1, a_2, a_3)$) 和 ($\vec{b} = (b_1, b_2, b_3)$),那么叉乘的计算公式为:
-
具体顺序:模型位于局部坐标系下的坐标,经过了Model Transform变为了世界坐标系下的坐标;由于需要相机的存在,因此需要连通世界空间中的所有物体,连同相机一起变换,变换的目的就是将相机转到标准位置,相机的标准位置是:位置位于坐标原点处,看向-Z轴,头顶为Y轴,这样就可以得到相机坐标系下的坐标。相机坐标系下的坐标经过透视投影变换(正交投影或者是透视投影)转换到了近平面的屏幕坐标,【为什么需要透视除法:①将齐次坐标转为欧氏几何坐标②实现透视缩放效果:即w分量比较大的经过透视除法后比较小?】。经过透视除法之后将坐标转换为了NDC坐标。NDC坐标经过视口变换之后,将NDC坐标映射到了所定义的视口矩阵上,即如果定义了一个视口矩阵
GL_VIEWPORT(x,y,w,h,n,f)那么最终的左边会被转到范围为$x \in(x, x + w),y \in (y,y+h), z \in(n,f)$。经过了视口变换之后,一个最终的屏幕坐标会被映射到所定义屏幕的一个像素上,就可以进行光栅化和着色了。 -
在离屏渲染上,需要先定义一个窗口(图片)的
aspect_ratio之后在定义视口的aspect_ratio-
纵横比的定义:
- 纵横比通常指的是图像的宽度与高度的比例。例如,16:9 的纵横比意味着图像的宽度是高度的 16/9 倍。
-
理想纵横比与实际纵横比:
-
aspect_ratio被设置为一个理想的比例值,但这并不意味着它总是与图像的实际宽度和高度完全匹配。这是因为图像的高度(image_height)必须是整数像素值,而不能是小数。
-
-
高度的整数限制:
- 由于图像的高度必须是整数,所以不能直接使用
aspect_ratio来计算高度,因为这可能导致非整数的高度值。相反,高度通常是根据宽度来计算的,然后向下取整到最近的整数。
- 由于图像的高度必须是整数,所以不能直接使用
-
高度向下取整的影响:
- 当高度向下取整时,实际的纵横比可能会比理想的纵横比要大。例如,如果理想的纵横比是 16:9,但高度取整后导致高度变小,那么实际的纵横比就会变大。
-
最小高度限制:
- 文本还提到了一个额外的限制,即不允许图像的高度小于一。这意味着即使计算出的高度值小于一,它也会被设置为至少一像素高。这同样会影响实际的纵横比。
-
基于宽度计算高度:
- 为了保证图像的纵横比尽可能接近理想的纵横比,开发者通常会首先设置图像的宽度,然后根据这个宽度和理想的纵横比来计算高度,最后将高度向下取整到最近的整数。
-
纵横比的近似:
- 由于上述原因,实际的纵横比是对理想纵横比的一个近似。开发者需要意识到这种差异,并在设计渲染流程时考虑到这一点。
-
纵横比的定义:
-
解释什么是
focal length:就是焦距的定义:即相机中心到视口平面中心的垂直距离-
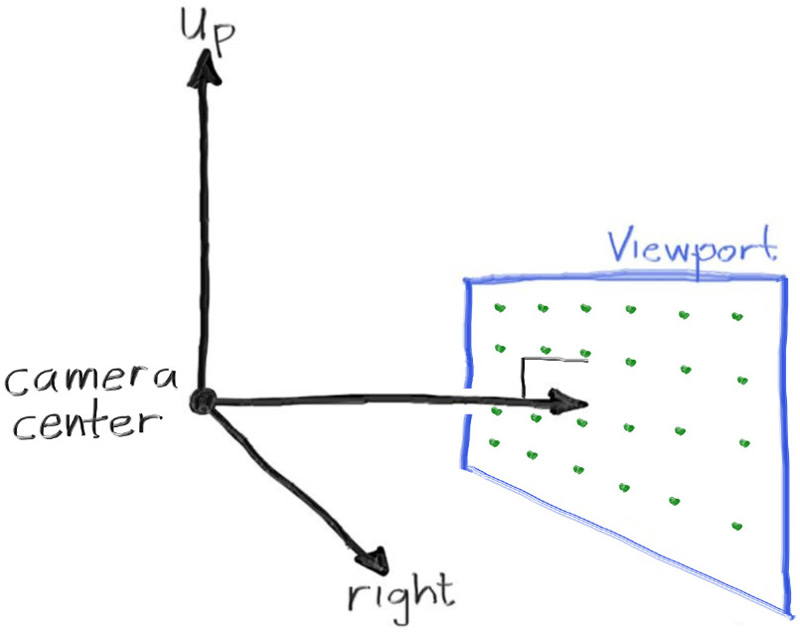
define the camera center: a point in 3D space from which all scene rays will originate (this is also commonly referred to as the eye point).
-
The vector from the camera center to the viewport center will be orthogonal to the viewport. We'll initially set the distance between the viewport and the camera center point to be one unit. This distance is often referred to as the focal length.
-
对于相机参数而言,焦距是镜头的物理数学;对于渲染而言,焦距是一个参数,用于控制渲染效果和视角FOV
-
焦距定义:焦距是相机镜头和成像平面(视口平面)之间的垂直距离
-
焦距会影响FOV(视场Filed Of View):较小的焦距可以捕获较大的视场,反之
-
FOV和焦距之间的计算关系为
- 对于垂直方向上有:$\tan(\frac{FOV_y}{2})=\frac{\frac{视口平面的高度}{2}}{焦距}$
- 对于水平方向上有:$\tan(\frac{FOV_x}{2})=\frac{\frac{视口平面的宽度}{2}}{焦距}$
-
一个简单的图示