14、Matrix.md

Matrix原理

自定义View系列目录

一、Matrix结构

在Android开发中，矩阵是一个非常强大且有趣的工具，在之前的一篇文章中对ColorMatrix的原理进行了详细的分析，用其实现了一些简单的颜色过滤功能，这一次我们来探寻一下同样强大的Matrix，它具有更改图像图形的有趣功能。我们先来看看Matrix的结构。


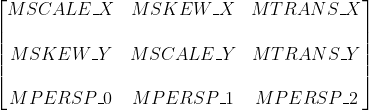
我们可以看到Matrix是一个3X3的矩阵。

• MSCALE_X、MSCALE_Y、MPERSP_2 分别表示X、Y、w(透视)的缩放
• MSKEW_X、MSKEW_Y 分别表示X、Y的错切
• MTRANS_X、MTRANS_Y 分别表示X、Y的平移
• MPERSP_0、MPERSP_1 分别表示X、Y方向上的透视

使用示例

在Android的很多地方其实都使用到了Matrix的方法，比如图片、Canvas、动画等，我们这里以图片为例，像在Canvas与ValueAnimator章节中一样，在onDraw函数中我们先绘制一个坐标系，然后来绘制一个矩形。

// 平移画布
canvas.translate(mWidth/2,mHeight/2);
mPaint.setStrokeWidth(1);// 恢复画笔默认宽度
// 绘制X轴
canvas.drawLine(-mWidth/2*0.8f,0,mWidth/2*0.8f,0,mPaint);
// 绘制Y轴
canvas.drawLine(0,-mHeight/2*0.8f,0,mHeight/2*0.8f,mPaint);
mPaint.setStrokeWidth(3);
// 绘制X轴箭头
canvas.drawLines(new float[]{
        mWidth/2*0.8f,0,mWidth/2*0.8f*0.95f,-mWidth/2*0.8f*0.05f,
        mWidth/2*0.8f,0,mWidth/2*0.8f*0.95f,mWidth/2*0.8f*0.05f
},mPaint);
// 绘制Y轴箭头
canvas.drawLines(new float[]{
        0,mHeight/2*0.8f,mWidth/2*0.8f*0.05f,mHeight/2*0.8f-mWidth/2*0.8f*0.05f,
        0,mHeight/2*0.8f,-mWidth/2*0.8f*0.05f,mHeight/2*0.8f-mWidth/2*0.8f*0.05f,
},mPaint);
// 创建矩阵
mMatrix = new Matrix();
/**
 *  测试的Matrix操作
 */

// 绘制图片
canvas.drawBitmap(mBitmap,mMatrix,null);

二、Matrix原理

1、缩放变换

将点的X轴和y轴方向分别缩放和倍。x、y的计算结果为 :


用矩阵表示 :

![](http://latex.codecogs.com/png.latex? $$ \left [ \begin{matrix} x\\ y\\ 1 \end{1} \right ]

\left [ \begin{matrix}
k_0 & 0 & 0 \\ 0 & k_1 & 0 \\ 0 & 0 & 1 \end{1} \right ] \left [ \begin{matrix} x_0\\ y_0\\ 1 \end{1} \right ] $$)

效果如图所示 :

使用示例

现在我们使用Matrix自带的setScale方法 :

/**
 *  测试的Matrix操作
 */
mMatrix.setScale(0.5f,0.5f);

Log.d("TAG",mMatrix.toString());

// Log
D/TAG: Matrix{[0.5, 0.0, 0.0][0.0, 0.5, 0.0][0.0, 0.0, 1.0]}

2、错切变换

错切变换的效果就是让所有点的x坐标(或者y坐标)保持不变，而对于的y坐标(或者x坐标)则按照比例发生平移。

水平错切

保持y不变，但其x坐标则按比例发生平移。x、y的计算结果为 :


用矩阵表示 :

![](http://latex.codecogs.com/png.latex? $$ \left [ \begin{matrix} x\\ y\\ 1 \end{1} \right ]

\left [ \begin{matrix}
1 & k & 0 \\ 0 & 1 & 0 \\ 0 & 0 & 1 \end{1} \right ] \left [ \begin{matrix} x_0\\ y_0\\ 1 \end{1} \right ] $$)

效果如图所示 :

垂直错切

保持x不变，但其y坐标则按比例发生平移。x、y的计算结果为 :


用矩阵表示 :

![](http://latex.codecogs.com/png.latex? $$ \left [ \begin{matrix} x\\ y\\ 1 \end{1} \right ]

\left [ \begin{matrix}
1 & 0 & 0 \\ k & 1 & 0 \\ 0 & 0 & 1 \end{1} \right ] \left [ \begin{matrix} x_0\\ y_0\\ 1 \end{1} \right ] $$)

效果如图所示 :

当然你也可以同时进行水平错切和垂直错切的变换。

使用示例

现在我们使用Matrix自带的setSkew方法 :

/**
 *  测试的Matrix操作
 */
mMatrix.setSkew(0f,0.5f);
Log.d("TAG",mMatrix.toString());

// Log
D/TAG: Matrix{[1.0, 0.0, 0.0][0.5, 1.0, 0.0][0.0, 0.0, 1.0]}

3、平移变换

假设有坐标为[](http://latex.codecogs.com/png.latex?$$ x_0、y_0 $$)，将其点进行平移，移动到点[](http://latex.codecogs.com/png.latex?$$ x、y $$)，其x、y计算结果为 :


用矩阵表示 :

![](http://latex.codecogs.com/png.latex? $$ \left [ \begin{matrix} x\\ y\\ 1 \end{1} \right ]

\left [ \begin{matrix}
1 & 0 & \Delta x \\ 0 & 1 & \Delta y \\ 0 & 0 & 1 \end{1} \right ] \left [ \begin{matrix} x_0\\ y_0\\ 1 \end{1} \right ] $$)

效果如图所示 :

使用示例

现在我们使用Matrix自带的setTranslate方法 :

/**
 *  测试的Matrix操作
 */
mMatrix.setTranslate(-200,-200);
Log.d("TAG",mMatrix.toString());

// Log
D/TAG: Matrix{[1.0, 0.0, -200.0][0.0, 1.0, -200.0][0.0, 0.0, 1.0]}

4、旋转变换

假设有一点坐标为[](http://latex.codecogs.com/png.latex?$$ x_0、y_0 $$)，距离原点为r，与x轴方向的夹角为α，绕原点旋转θ后，变换为点[](http://latex.codecogs.com/png.latex?$$ x、y $$)，其变换前后各点计算结果为 :

 = r \cdot\cos\alpha\cos\theta - r \cdot\sin\alpha\sin\theta = x_0\cos\theta - y_0\sin\theta $$)
 = r \cdot\sin\alpha\cos\theta + r \cdot\cos\alpha\sin\theta = y_0\cos\theta + x_0\sin\theta $$)

用矩阵表示为 :

![](http://latex.codecogs.com/png.latex? $$ \left [ \begin{matrix} x\\ y\\ 1 \end{1} \right ]

\left [ \begin{matrix}
\cos\theta & -\sin\theta & 0 \\ \sin\theta & \cos\theta & 0 \\ 0 & 0 & 1 \end{1} \right ] \left [ \begin{matrix} x_0\\ y_0\\ 1 \end{1} \right ] $$)

效果如图所示 :

使用示例

现在我们使用Matrix自带的setRotate方法 :

/**
 *  测试的Matrix操作
 */
mMatrix.setRotate(180);
Log.d("TAG",mMatrix.toString());

// Log
D/TAG: Matrix{[-1.0, -0.0, 0.0][0.0, -1.0, 0.0][0.0, 0.0, 1.0]}

5、透视变换

我们在之前的变换中，一直没有说到最后一行的三个参数MPERSP_0、MPERSP_1、MPERSP_2，这里我们来稍微聊聊这三个参数所表示的透视。我们一般在图像中的一个点将使用如下方式进行表示(x, y, w),而Android中的二维矩阵计算是基于齐次坐标的，齐次坐标要求w的值为1，所以这个点的表示方法就变化为(x/w, y/w, 1)。
透视变换的效果其实类似于投影机的方式，我们看下w=3时，坐标(15,21,3)的效果 :

现在看下(15,21,3)计算出的齐次坐标系坐标(5,7,1)的效果 :

根据这个规则，也就解释了我们在使用过程中修改MPERSP_2参数时，图像会发生的类似缩放的效果，其实就是透视变换的效果。

使用示例

现在我们使用Matrix自带的setValues方法 :

/**
 *  测试的Matrix操作
 */
mMatrix.setValues(new float[]{1, 0, 0, 0, 1, 0, 0, 0, 1.5f});
Log.d("TAG",mMatrix.toString());

// Log
D/TAG: Matrix{[1.0, 0.0, 0.0][0.0, 1.0, 0.0][0.0, 0.0, 1.5]}

三、Matrix前乘与后乘

Matrix前乘与后乘的情况跟我在之前的文章ColorMatrix详解中ColorMatrix相乘章节所描述的基本相同。

前乘

前乘相当于，当前矩阵乘以输入的矩阵

示例如下:

mMatrix.reset();
mMatrix.preScale(sx,sy);
mMatrix.preTranslate(tx,ty);

用矩阵表示为 :

![](http://latex.codecogs.com/png.latex? $$ \left [ \begin{matrix} & &\\ & Result & Matrix &\\ & & \end{1} \right ]

\left [ \begin{matrix} & &\\ & Initial & Matrix &\\ & & \end{1} \right ] \left [ \begin{matrix} sx & 0 & 0 \\ 0 & sy & 0 \\ 0 & 0 & 1 \end{1} \right ]
\left [ \begin{matrix}
1 & 0 & tx \\ 0 & 1 & ty \\ 0 & 0 & 1 \end{1} \right ] $$)

后乘

后乘相当于，输入的矩阵乘以当前矩阵

mMatrix.reset();
mMatrix.postScale(sx,sy);
mMatrix.postTranslate(tx,ty);

![](http://latex.codecogs.com/png.latex? $$ \left [ \begin{matrix} & &\\ & Result & Matrix &\\ & & \end{1} \right ]

\left [ \begin{matrix} 1 & 0 & tx \\ 0 & 1 & ty \\ 0 & 0 & 1 \end{1} \right ] \left [ \begin{matrix} sx & 0 & 0 \\ 0 & sy & 0 \\ 0 & 0 & 1 \end{1} \right ]
\left [ \begin{matrix}
& &\\ & Initial & Matrix &\\ & & \end{1} \right ] $$)

四、总结

本文深入分析了Matrix的原理，并讲解了其常用方法和前后乘的方法。如果在阅读过程中，有任何疑问与问题，欢迎与我联系。
博客:www.idtkm.com
GitHub:https://github.com/Idtk
微博:http://weibo.com/Idtk
邮箱:IdtkMa@gmail.com

参考

Matrix
Android Matrix
Android中关于矩阵（Matrix）前乘后乘的一些认识
齐次坐标系入门级思考
次坐标和投影
变换矩阵