作者微博: @GcsSloop
相关文章: 自定义View目录
本篇依旧属于Matrix,主要讲解Camera,Android下有很多相机应用,其中的美颜相机更是不少,不过今天这个Camera可不是我们平时拍照的那个相机,而是graphic包下的Camera,专业给View拍照的相机,不过既然是相机,作用都是类似的,主要是将3D的内容拍扁变成2D的内容。
众所周知,我们的手机屏幕是一个2D的平面,所以也没办法直接显示3D的信息,因此我们看到的所有3D效果都是3D在2D平面的投影而已,而本文中的Camera主要作用就是这个,将3D信息转换为2D平面上的投影,实际上这个类更像是一个操作Matrix的工具类,使用Camera和Matrix可以在不使用OpenGL的情况下制作出简单的3D效果。
| 方法类别 | 相关API | 简介 |
|---|---|---|
| 基本方法 | save、restore | 保存、 回滚 |
| 常用方法 | getMatrix、applyToCanvas | 获取Matrix、应用到画布 |
| 平移 | translate | 位移 |
| 旋转 | rotate (API 12)、rotateX、rotateY、rotateZ | 各种旋转 |
| 相机位置 | setLocation (API 12)、getLocationX (API 16)、getLocationY (API 16)、getLocationZ (API 16) | 设置与获取相机位置 |
Camera的方法并不是特别多,很多内容与之前的讲解的Canvas和Matrix类似,不过又稍有不同,之前的画布操作和Matrix主要是作用于2D空间,而Camera则主要作用于3D空间。
在具体讲解方法之前,先补充几个基础概念,以便于后面理解。
我们Camera使用的3维坐标系是左手坐标系,即左手手臂指向x轴正方向,四指弯曲指向y轴正方向,此时展开大拇指指向的方向是z轴正方向。
至于为什么要用左手坐标系呢?~~大概是因为赶工的时候右手不方便比划吧,大雾。~~实际上不同平台上使用的坐标系也有不同,有的是左手,有的是右手,貌似并没有统一的标准,只需要记住 Android 平台上面使用的是左手坐标系即可。
2D 和 3D 坐标是通过Matrix关联起来的,所以你可以认为两者是同一个坐标系,但又有差别,重点就是y轴方向不同。
| 坐标系 | 2D坐标系 | 3D坐标系 |
|---|---|---|
| 原点默认位置 | 左上角 | 左上角 |
| X 轴默认方向 | 右 | 右 |
| Y 轴默认方向 | 下 | 上 |
| Z 轴默认方向 | 无 | 垂直屏幕向内 |
3D坐标系在屏幕中各个坐标轴默认方向展示:
注意y轴默认方向是向上,而2D则是向下,另外本图不代表3D坐标系实际位置。
三维投影是将三维空间中的点映射到二维平面上的方法。由于目前绝大多数图形数据的显示方式仍是二维的,因此三维投影的应用相当广泛,尤其是在计算机图形学,工程学和工程制图中。
三维投影一般有两种,正交投影 和 透视投影。
- 正交投影就是我们数学上学过的 "正视图、正视图、侧视图、俯视图" 这些东西。
- 透视投影则更像拍照片,符合近大远小的关系,有立体感,我们此处使用的就是透视投影。
如果你学过Unity,那么你对摄像机这一个概念应该会有比较透彻的理解。在一个虚拟的3D的立体空间中,由于我们无法直接用眼睛去观察这一个空间,所以要借助摄像机采集信息,制成2D影像供我们观察。简单来说,摄像机就是我们观察虚拟3D空间的眼睛。
Android 上面观察View的摄像机默认位置在屏幕左上角,而且是距屏幕有一段距离的,假设灰色部分是手机屏幕,白色是上面的一个View,摄像机位置看起来大致就是下面这样子的(为了更好的展示摄像机的位置,做了一个空间转换效果的动图)。
摄像机的位置默认是 (0, 0, -576)。其中 -576= -8 x 72,虽然官方文档说距离屏幕的距离是 -8, 但经过测试实际距离是 -576 像素,当距离为 -10 的时候,实际距离为 -720 像素。我使用了3款手机测试,屏幕大小和像素密度均不同,但结果都是一样的。
这个魔数可以在 Android 底层的图像引擎 Skia 中找到。在 Skia 中,Camera 的位置单位是英寸,英寸和像素的换算单位在 Skia 中被固定为 72 像素,而 Android 中把这个换算单位照搬了过来。
基本方法就有两个save 和restore,主要作用为保存当前状态和恢复到上一次保存的状态,通常成对使用,常用格式如下:
camera.save(); // 保存状态
... // 具体操作
camera.retore(); // 回滚状态这两个方法是Camera中最基础也是最常用的方法。
void getMatrix (Matrix matrix)计算当前状态下矩阵对应的状态,并将计算后的矩阵赋值给参数matrix。
void applyToCanvas (Canvas canvas)计算当前状态下单矩阵对应的状态,并将计算后的矩阵应用到指定的canvas上。
声明:以下示例中 Matrix 的平移均使用 postTranslate 来演示,实际情况中使用set、pre 或 post 需要视情况而定。
void translate (float x, float y, float z)和2D平移类似,只不过是多出来了一个维度,从只能在2D平面上平移到在3D空间内平移,不过,此处仍有几个要点需要重点对待。
camera.translate(x, 0, 0);
matrix.postTranslate(x, 0);两者x轴同向,所以 Camera 和 Matrix 在沿x轴平移上是一致的。
结论:
一致是指平移方向和平移距离一致,在默认情况下,上面两种均可以让坐标系向右移动x个单位。
这个就有点意思了,两个坐标系相互关联,但是两者的y轴方向是相反的,很容易把人搞迷糊。你可以这么玩:
Camera camera = new Camera();
camera.translate(0, 100, 0); // camera - 沿y轴正方向平移100像素
Matrix matrix = new Matrix();
camera.getMatrix(matrix);
matrix.postTranslate(0,100); // matrix - 沿y轴正方向平移100像素
Log.i(TAG, "Matrix: "+matrix.toShortString());在上面这种写法,虽然用了5行代码,但是效果却和 Matrix matrix = new Matrix(); 一样,结果都是单位矩阵。而且看起来貌似没有啥问题,毕竟两次平移都是正向100。(如果遇见不懂技术的领导嫌你写代码量少,你可以这样多写几遍,反正一般人是看不出问题的。)
Matrix: [1.0, 0.0, 0.0][0.0, 1.0, 0.0][0.0, 0.0, 1.0]
结论:
由于两者y轴相反,所以 camera.translate(0, -y, 0); 与 matrix.postTranslate(0, y);平移方向和距离一致,在默认情况下,这两种方法均可以让坐标系向下移动y个单位。
这个不仅有趣,还容易蒙逼,上面两种情况再怎么闹腾也只是在2D平面上,而z轴的出现则让其有了空间感。
当View和摄像机在同一条直线上时: 此时沿z轴平移相当于缩放的效果,缩放中心为摄像机所在(x, y)坐标,当View接近摄像机时,看起来会变大,远离摄像机时,看起来会变小,近大远小。
当View和摄像机不在同一条直线上时: 当View远离摄像机的时候,View在缩小的同时也在不断接近摄像机在屏幕投影位置(通常情况下为Z轴,在平面上表现为接近坐标原点)。相反,当View接近摄像机的时候,View在放大的同时会远离摄像机在屏幕投影位置。
我知道,这样说你们肯定是蒙逼的,话说为啥远离摄像机的时候会接近摄像机在屏幕投影位置(´・_・`),肯定觉得我在逗你们玩,完全是前后矛盾,逻辑都不通,不过这个在这里的确是不矛盾的,因为远离是在3D空间里的情况,而接近只是在2D空间的投影,看下图。
假设大矩形是手机屏幕,白色小矩形是View,摄像机位于屏幕左上角,请注意上面View与摄像机的距离以及下方View的大小以及距离左上角(摄像机在屏幕投影位置)的距离。
至于为什么会这样,因为我们人眼视觉就是这样的,当我们看向远方的时候,视线最终都会消失在视平线上,如果你站在两条平行线中间,看起来它们会在远方(视平线上)相交,虽然在3D空间上两者距离不变,但在2D投影上却是越来越接近,如下图(图片来自网络):
结论:
关于3D效果的平移说起来比较麻烦,但你可以自己实际的体验一下,毕竟我们是生活在3D空间的,拿一张纸片来模拟View,用眼睛当做摄像机,在眼前来回移动纸片,多试几次大致就明白是怎么回事了。
| 平移 | 重点内容 |
|---|---|
| x轴 | 2D 和 3D 相同。 |
| y轴 | 2D 和 3D 相反。 |
| z轴 | 近大远小、视线相交。 |
旋转是Camera制作3D效果的核心,不过它制作出来的并不能算是真正的3D,而是伪3D,因为View是没有厚度的。
// (API 12) 可以控制View同时绕x,y,z轴旋转,可以由下面几种方法复合而来。
void rotate (float x, float y, float z);
// 控制View绕单个坐标轴旋转
void rotateX (float deg);
void rotateY (float deg);
void rotateZ (float deg);这个东西瞎扯理论也不好理解,直接上图:
以上三张图分别为,绕x轴,y轴,z轴旋转的情况,至于为什么没有显示z轴,是因为z轴是垂直于手机屏幕的,在屏幕上的投影就是一个点。
关于旋转,有以下几点需要注意:
旋转中心默认是坐标原点,对于图片来说就是左上角位置。
我们都知道,在2D中,不论是旋转,错切还是缩放都是能够指定操作中心点位置的,但是在3D中却没有默认的方法,如果我们想要让图片围绕中心点旋转怎么办? 这就要使用到我们在Matrix原理提到过的方法,虽然当时因为有更好的选择方案,并不提倡这样做:
Matrix temp = new Matrix(); // 临时Matrix变量
this.getMatrix(temp); // 获取Matrix
temp.preTranslate(-centerX, -centerY); // 使用pre将旋转中心移动到和Camera位置相同。
temp.postTranslate(centerX, centerY); // 使用post将图片(View)移动到原来的位置说到3D旋转,最经典的应该就是ApiDemo里面的 Rotate3dAnimation 了,见过不少博文都是根据Rotate3dAnimation修改的效果,这是一个非常经典的例子,鉴于代码也不长,就贴在这里和大家一起品鉴一下。
public class Rotate3dAnimation extends Animation {
private final float mFromDegrees;
private final float mToDegrees;
private final float mCenterX;
private final float mCenterY;
private final float mDepthZ;
private final boolean mReverse;
private Camera mCamera;
/**
* 创建一个绕y轴旋转的3D动画效果,旋转过程中具有深度调节,可以指定旋转中心。
*
* @param fromDegrees 起始时角度
* @param toDegrees 结束时角度
* @param centerX 旋转中心x坐标
* @param centerY 旋转中心y坐标
* @param depthZ 最远到达的z轴坐标
* @param reverse true 表示由从0到depthZ,false相反
*/
public Rotate3dAnimation(float fromDegrees, float toDegrees,
float centerX, float centerY, float depthZ, boolean reverse) {
mFromDegrees = fromDegrees;
mToDegrees = toDegrees;
mCenterX = centerX;
mCenterY = centerY;
mDepthZ = depthZ;
mReverse = reverse;
}
@Override
public void initialize(int width, int height, int parentWidth, int parentHeight) {
super.initialize(width, height, parentWidth, parentHeight);
mCamera = new Camera();
}
@Override
protected void applyTransformation(float interpolatedTime, Transformation t) {
final float fromDegrees = mFromDegrees;
float degrees = fromDegrees + ((mToDegrees - fromDegrees) * interpolatedTime);
final float centerX = mCenterX;
final float centerY = mCenterY;
final Camera camera = mCamera;
final Matrix matrix = t.getMatrix();
camera.save();
// 调节深度
if (mReverse) {
camera.translate(0.0f, 0.0f, mDepthZ * interpolatedTime);
} else {
camera.translate(0.0f, 0.0f, mDepthZ * (1.0f - interpolatedTime));
}
// 绕y轴旋转
camera.rotateY(degrees);
camera.getMatrix(matrix);
camera.restore();
// 调节中心点
matrix.preTranslate(-centerX, -centerY);
matrix.postTranslate(centerX, centerY);
}
}可以看到,短短的几十行代码就完成了,而核心代码(有注释部分)仅仅几行而已,简洁易懂。不过呢,这一份代码依旧是一份未完成的代码(不然怎么叫ApiDemo呢?),并且很多人不知道怎么修改。
不知诸位在使用的时候可否发现了一个问题,同一份代码在不同手机上显示效果也是不同的,在像素密度较低的手机上,旋转效果比较正常,但是在像素密度较高的手机上显示效果则会很夸张,具体会怎样的,下面就来看一下具体效果。
可以看到,图片不仅因为形变失真,而且在中间一段因为形变过大导致图片无法显示,当然了,单个手机失真,你可以用depthZ忽悠过去,当 depthZ 设置的数值比较大大时候,图像在翻转同时会远离摄像头,距离比较远,失真就不会显得很严重,但这仍掩盖不了在不同手机上显示效果不同。
如何解决这一问题呢?
想要解决其实也不难,只要修改两个数值就可以了,这两个数值就是在Matrix中一直被众多开发者忽略的 MPERSP_0 和 MPERSP_1
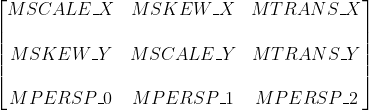
下面是修改后的代码(重点部分都已经标注出来了):
public class Rotate3dAnimation extends Animation {
private final float mFromDegrees;
private final float mToDegrees;
private final float mCenterX;
private final float mCenterY;
private final float mDepthZ;
private final boolean mReverse;
private Camera mCamera;
float scale = 1; // <------- 像素密度
/**
* 创建一个绕y轴旋转的3D动画效果,旋转过程中具有深度调节,可以指定旋转中心。
* @param context <------- 添加上下文,为获取像素密度准备
* @param fromDegrees 起始时角度
* @param toDegrees 结束时角度
* @param centerX 旋转中心x坐标
* @param centerY 旋转中心y坐标
* @param depthZ 最远到达的z轴坐标
* @param reverse true 表示由从0到depthZ,false相反
*/
public Rotate3dAnimation(Context context, float fromDegrees, float toDegrees,
float centerX, float centerY, float depthZ, boolean reverse) {
mFromDegrees = fromDegrees;
mToDegrees = toDegrees;
mCenterX = centerX;
mCenterY = centerY;
mDepthZ = depthZ;
mReverse = reverse;
// 获取手机像素密度 (即dp与px的比例)
scale = context.getResources().getDisplayMetrics().density;
}
@Override
public void initialize(int width, int height, int parentWidth, int parentHeight) {
super.initialize(width, height, parentWidth, parentHeight);
mCamera = new Camera();
}
@Override
protected void applyTransformation(float interpolatedTime, Transformation t) {
final float fromDegrees = mFromDegrees;
float degrees = fromDegrees + ((mToDegrees - fromDegrees) * interpolatedTime);
final float centerX = mCenterX;
final float centerY = mCenterY;
final Camera camera = mCamera;
final Matrix matrix = t.getMatrix();
camera.save();
// 调节深度
if (mReverse) {
camera.translate(0.0f, 0.0f, mDepthZ * interpolatedTime);
} else {
camera.translate(0.0f, 0.0f, mDepthZ * (1.0f - interpolatedTime));
}
// 绕y轴旋转
camera.rotateY(degrees);
camera.getMatrix(matrix);
camera.restore();
// 修正失真,主要修改 MPERSP_0 和 MPERSP_1
float[] mValues = new float[9];
matrix.getValues(mValues); //获取数值
mValues[6] = mValues[6]/scale; //数值修正
mValues[7] = mValues[7]/scale; //数值修正
matrix.setValues(mValues); //重新赋值
// 调节中心点
matrix.preTranslate(-centerX, -centerY);
matrix.postTranslate(centerX, centerY);
}
}修改后效果:
上下对比差别还是很大的,顺便附上测试代码吧,layout文件就不写了,随便放一个ImageView就行了。
setContentView(R.layout.activity_test_camera_rotate2);
ImageView view = (ImageView) findViewById(R.id.img);
assert view != null;
view.setOnClickListener(new View.OnClickListener() {
@Override
public void onClick(View v) {
// 计算中心点(这里是使用view的中心作为旋转的中心点)
final float centerX = v.getWidth() / 2.0f;
final float centerY = v.getHeight() / 2.0f;
//括号内参数分别为(上下文,开始角度,结束角度,x轴中心点,y轴中心点,深度,是否扭曲)
final Rotate3dAnimation rotation = new Rotate3dAnimation(MainActivity.this, 0, 180, centerX, centerY, 0f, true, 2);
rotation.setDuration(3000); //设置动画时长
rotation.setFillAfter(true); //保持旋转后效果
rotation.setInterpolator(new LinearInterpolator()); //设置插值器
v.startAnimation(rotation);
}
});我们可以使用translate和rotate来控制拍摄对象,也可以移动相机自身的位置,不过这些方法并不常用(看添加时间就知道啦)。
void setLocation (float x, float y, float z); // (API 12) 设置相机位置,默认位置是(0, 0, -8)
float getLocationX (); // (API 16) 获取相机位置的x坐标,下同
float getLocationY ();
float getLocationZ ();我们知道近大远小,而物体之间的距离是相对的,让物体远离相机和让相机远离物体结果是一样的,实际上设置相机位置基本可以使用translate替代。
虽然设置相机位置用处并不大,但还是要提几点注意事项:
这个比较容易理解,当你把一个物体和相机放在同一个位置的时候,相机是拍摄不到这个物体的,正如你拿一张卡片放在手机侧面,摄像头是拍摄不到的。
当View不断接近摄像机并越过摄像机位置时,仍能看到View,并且View大小会随着距离摄像机的位置越来越远而逐渐变小,你可以理解为它有前置摄像头和后置摄像头。
View的状态只取决于View和摄像机之间的相对位置,不过由于单位不同,摄像机平移一个单位等于View平移72个像素。下面两段代码是等价的:
Camera camera = new Camera();
camera.setLocation(1,0,-8); // 摄像机默认位置是(0, 0, -8)
Matrix matrix = new Matrix();
camera.getMatrix(matrix);
Log.e(TAG, "location: "+matrix.toShortString() );
Camera camera2 = new Camera();
camera2.translate(-72,0,0);
Matrix matrix2 = new Matrix();
camera2.getMatrix(matrix2);
Log.e(TAG, "translate: "+matrix2.toShortString() );结果:
location: [1.0, 0.0, -72.0][0.0, 1.0, 0.0][0.0, 0.0, 1.0]
translate: [1.0, 0.0, -72.0][0.0, 1.0, 0.0][0.0, 0.0, 1.0
- View显示状态取决于View和摄像机之间的相对位置
- View和相机的Z轴距离不能为0
小技巧:关于摄像机和View的位置,你可以打开手机后置摄像头,拿一张卡片来回的转动平移或者移动手机位置,观察卡片在屏幕上的变化,
本篇主要讲解了关于Camera和Matrix的一些基础知识,Camera运用得当的话是能够制造出很多炫酷的效果的,我这里算是抛砖引玉,推荐一些比较炫酷的控件。












