作者微博: @GcsSloop
相关文章: 自定义View目录
在上一篇文章中,我们对Matrix做了一个简单的了解,偏向理论,在本文中则会详细的讲解Matrix的具体用法,以及Matrix的一些实用技巧。
按照惯例,先放方法表做概览。
| 方法类别 | 相关API | 摘要 |
|---|---|---|
| 基本方法 | equals hashCode toString toShortString | 比较、 获取哈希值、 转换为字符串 |
| 数值操作 | set reset setValues getValues | 设置、 重置、 设置数值、 获取数值 |
| 数值计算 | mapPoints mapRadius mapRect mapVectors | 计算变换后的数值 |
| 设置(set) | setConcat setRotate setScale setSkew setTranslate | 设置变换 |
| 前乘(pre) | preConcat preRotate preScale preSkew preTranslate | 前乘变换 |
| 后乘(post) | postConcat postRotate postScale postSkew postTranslate | 后乘变换 |
| 特殊方法 | setPolyToPoly setRectToRect rectStaysRect setSinCos | 一些特殊操作 |
| 矩阵相关 | invert isAffine(API21) isIdentity | 求逆矩阵、 是否为仿射矩阵、 是否为单位矩阵 ... |
构造方法没有在上面表格中列出。
Matrix ()创建一个全新的Matrix,使用格式如下:
Matrix matrix = new Matrix();通过这种方式创建出来的并不是一个数值全部为空的矩阵,而是一个单位矩阵,如下:
Matrix (Matrix src)这种方法则需要一个已经存在的矩阵作为参数,使用格式如下:
Matrix matrix = new Matrix(src);创建一个Matrix,并对src深拷贝(理解为新的matrix和src是两个对象,但内部数值相同即可)。
基本方法内容比较简单,在此处简要介绍一下。
比较两个Matrix的数值是否相同。
获取Matrix的哈希值。
将Matrix转换为字符串: Matrix{[1.0, 0.0, 0.0][0.0, 1.0, 0.0][0.0, 0.0, 1.0]}
将Matrix转换为短字符串: [1.0, 0.0, 0.0][0.0, 1.0, 0.0][0.0, 0.0, 1.0]
数值操作这一组方法可以帮助我们直接控制Matrix里面的数值。
void set (Matrix src)没有返回值,有一个参数,作用是将参数Matrix的数值复制到当前Matrix中。如果参数为空,则重置当前Matrix,相当于reset()。
void reset ()重置当前Matrix(将当前Matrix重置为单位矩阵)。
void setValues (float[] values)setValues的参数是浮点型的一维数组,长度需要大于9,拷贝数组中的前9位数值赋值给当前Matrix。
void getValues (float[] values)很显然,getValues和setValues是一对方法,参数也是浮点型的一维数组,长度需要大于9,将Matrix中的数值拷贝进参数的前9位中。
void mapPoints (float[] pts)
void mapPoints (float[] dst, float[] src)
void mapPoints (float[] dst, int dstIndex,float[] src, int srcIndex, int pointCount)计算一组点基于当前Matrix变换后的位置,(由于是计算点,所以参数中的float数组长度一般都是偶数的,若为奇数,则最后一个数值不参与计算)。
它有三个重载方法:
(1) void mapPoints (float[] pts) 方法仅有一个参数,pts数组作为参数传递原始数值,计算结果仍存放在pts中。
示例:
// 初始数据为三个点 (0, 0) (80, 100) (400, 300)
float[] pts = new float[]{0, 0, 80, 100, 400, 300};
// 构造一个matrix,x坐标缩放0.5
Matrix matrix = new Matrix();
matrix.setScale(0.5f, 1f);
// 输出pts计算之前数据
Log.i(TAG, "before: "+ Arrays.toString(pts));
// 调用map方法计算
matrix.mapPoints(pts);
// 输出pts计算之后数据
Log.i(TAG, "after : "+ Arrays.toString(pts));结果:
before: [0.0, 0.0, 80.0, 100.0, 400.0, 300.0]
after : [0.0, 0.0, 40.0, 100.0, 200.0, 300.0]
(2) void mapPoints (float[] dst, float[] src) ,src作为参数传递原始数值,计算结果存放在dst中,src不变。
如果原始数据需要保留则一般使用这种方法。
示例:
// 初始数据为三个点 (0, 0) (80, 100) (400, 300)
float[] src = new float[]{0, 0, 80, 100, 400, 300};
float[] dst = new float[6];
// 构造一个matrix,x坐标缩放0.5
Matrix matrix = new Matrix();
matrix.setScale(0.5f, 1f);
// 输出计算之前数据
Log.i(TAG, "before: src="+ Arrays.toString(src));
Log.i(TAG, "before: dst="+ Arrays.toString(dst));
// 调用map方法计算
matrix.mapPoints(dst,src);
// 输出计算之后数据
Log.i(TAG, "after : src="+ Arrays.toString(src));
Log.i(TAG, "after : dst="+ Arrays.toString(dst));结果:
before: src=[0.0, 0.0, 80.0, 100.0, 400.0, 300.0]
before: dst=[0.0, 0.0, 0.0, 0.0, 0.0, 0.0]
after : src=[0.0, 0.0, 80.0, 100.0, 400.0, 300.0]
after : dst=[0.0, 0.0, 40.0, 100.0, 200.0, 300.0]
(3) void mapPoints (float[] dst, int dstIndex,float[] src, int srcIndex, int pointCount) 可以指定只计算一部分数值。
| 参数 | 摘要 |
|---|---|
| dst | 目标数据 |
| dstIndex | 目标数据存储位置起始下标 |
| src | 源数据 |
| srcIndex | 源数据存储位置起始下标 |
| pointCount | 计算的点个数 |
示例:
将第二、三个点计算后存储进dst最开始位置。
// 初始数据为三个点 (0, 0) (80, 100) (400, 300)
float[] src = new float[]{0, 0, 80, 100, 400, 300};
float[] dst = new float[6];
// 构造一个matrix,x坐标缩放0.5
Matrix matrix = new Matrix();
matrix.setScale(0.5f, 1f);
// 输出计算之前数据
Log.i(TAG, "before: src="+ Arrays.toString(src));
Log.i(TAG, "before: dst="+ Arrays.toString(dst));
// 调用map方法计算(最后一个2表示两个点,即四个数值,并非两个数值)
matrix.mapPoints(dst, 0, src, 2, 2);
// 输出计算之后数据
Log.i(TAG, "after : src="+ Arrays.toString(src));
Log.i(TAG, "after : dst="+ Arrays.toString(dst));结果:
before: src=[0.0, 0.0, 80.0, 100.0, 400.0, 300.0]
before: dst=[0.0, 0.0, 0.0, 0.0, 0.0, 0.0]
after : src=[0.0, 0.0, 80.0, 100.0, 400.0, 300.0]
after : dst=[40.0, 100.0, 200.0, 300.0, 0.0, 0.0]
float mapRadius (float radius)测量半径,由于圆可能会因为画布变换变成椭圆,所以此处测量的是平均半径。
示例:
float radius = 100;
float result = 0;
// 构造一个matrix,x坐标缩放0.5
Matrix matrix = new Matrix();
matrix.setScale(0.5f, 1f);
Log.i(TAG, "mapRadius: "+radius);
result = matrix.mapRadius(radius);
Log.i(TAG, "mapRadius: "+result);结果:
mapRadius: 100.0
mapRadius: 70.71068
boolean mapRect (RectF rect)
boolean mapRect (RectF dst, RectF src)
测量矩形变换后位置。
(1) boolean mapRect (RectF rect) 测量rect并将测量结果放入rect中,返回值是判断矩形经过变换后是否仍为矩形。
示例:
RectF rect = new RectF(400, 400, 1000, 800);
// 构造一个matrix
Matrix matrix = new Matrix();
matrix.setScale(0.5f, 1f);
matrix.postSkew(1,0);
Log.i(TAG, "mapRadius: "+rect.toString());
boolean result = matrix.mapRect(rect);
Log.i(TAG, "mapRadius: "+rect.toString());
Log.e(TAG, "isRect: "+ result);结果:
mapRadius: RectF(400.0, 400.0, 1000.0, 800.0)
mapRadius: RectF(600.0, 400.0, 1300.0, 800.0)
isRect: false
由于使用了错切,所以返回结果为false。
(2) boolean mapRect (RectF dst, RectF src) 测量src并将测量结果放入dst中,返回值是判断矩形经过变换后是否仍为矩形,和之前没有什么太大区别,此处就不啰嗦了。
测量向量。
void mapVectors (float[] vecs)
void mapVectors (float[] dst, float[] src)
void mapVectors (float[] dst, int dstIndex, float[] src, int srcIndex, int vectorCount)mapVectors 与 mapPoints 基本上是相同的,可以直接参照上面的mapPoints使用方法。
而两者唯一的区别就是mapVectors不会受到位移的影响,这符合向量的定律,如果你不了解的话,请找到以前教过你的老师然后把学费要回来。
区别:
float[] src = new float[]{1000, 800};
float[] dst = new float[2];
// 构造一个matrix
Matrix matrix = new Matrix();
matrix.setScale(0.5f, 1f);
matrix.postTranslate(100,100);
// 计算向量, 不受位移影响
matrix.mapVectors(dst, src);
Log.i(TAG, "mapVectors: "+Arrays.toString(dst));
// 计算点
matrix.mapPoints(dst, src);
Log.i(TAG, "mapPoints: "+Arrays.toString(dst));结果:
mapVectors: [500.0, 800.0]
mapPoints: [600.0, 900.0]
对于四种基本变换 平移(translate)、缩放(scale)、旋转(rotate)、 错切(skew) 它们每一种都三种操作方法,分别为 设置(set)、 前乘(pre) 和 后乘 (post)。而它们的基础是Concat,通过先构造出特殊矩阵然后用原始矩阵Concat特殊矩阵,达到变换的结果。
关于四种基本变换的知识和三种对应操作的区别,详细可以参考 Canvas之画布操作 和 Matrix原理 这两篇文章的内容。
由于之前的文章已经详细的讲解过了它们的原理与用法,所以此处就简要的介绍一下:
| 方法 | 简介 |
|---|---|
| set | 设置,会覆盖掉之前的数值,导致之前的操作失效。 |
| pre | 前乘,相当于矩阵的右乘, M' = M * S (S指为特殊矩阵) |
| post | 后乘,相当于矩阵的左乘,M' = S * M (S指为特殊矩阵) |
Matrix 相关的重要知识:
-
1.一开始从Canvas中获取到到Matrix并不是初始矩阵,而是经过偏移后到矩阵,且偏移距离就是距离屏幕左上角的位置。
-
这个可以用于判定View在屏幕上的绝对位置,View可以根据所处位置做出调整。
-
2.构造Matrix时使用的是矩阵乘法,前乘(pre)与后乘(post)结果差别很大。
-
这个直接参见上一篇文章 Matrix原理 即可。
-
3.受矩阵乘法影响,后面的执行的操作可能会影响到之前的操作。
-
使用时需要注意构造顺序。
这一类方法看似不起眼,但拿来稍微加工一下就可能制作意想不到的效果。
boolean setPolyToPoly (
float[] src, // 原始数组 src [x,y],存储内容为一组点
int srcIndex, // 原始数组开始位置
float[] dst, // 目标数组 dst [x,y],存储内容为一组点
int dstIndex, // 目标数组开始位置
int pointCount) // 测控点的数量 取值范围是: 0到4Poly全称是Polygon,多边形的意思,了解了意思大致就能知道这个方法是做什么用的了,应该与PS中自由变换中的扭曲有点类似。
从参数我们可以了解到setPolyToPoly最多可以支持4个点,这四个点通常为图形的四个角,可以通过这四个角将视图从矩形变换成其他形状。
简单示例:
public class MatrixSetPolyToPolyTest extends View {
private Bitmap mBitmap; // 要绘制的图片
private Matrix mPolyMatrix; // 测试setPolyToPoly用的Matrix
public MatrixSetPolyToPolyTest(Context context) {
super(context);
initBitmapAndMatrix();
}
private void initBitmapAndMatrix() {
mBitmap = BitmapFactory.decodeResource(getResources(),
R.drawable.poly_test);
mPolyMatrix = new Matrix();
float[] src = {0, 0, // 左上
mBitmap.getWidth(), 0, // 右上
mBitmap.getWidth(), mBitmap.getHeight(), // 右下
0, mBitmap.getHeight()}; // 左下
float[] dst = {0, 0, // 左上
mBitmap.getWidth(), 400, // 右上
mBitmap.getWidth(), mBitmap.getHeight() - 200, // 右下
0, mBitmap.getHeight()}; // 左下
// 核心要点
mPolyMatrix.setPolyToPoly(src, 0, dst, 0, src.length >> 1); // src.length >> 1 为位移运算 相当于处以2
// 此处为了更好的显示对图片进行了等比缩放和平移(图片本身有点大)
mPolyMatrix.postScale(0.26f, 0.26f);
mPolyMatrix.postTranslate(0,200);
}
@Override
protected void onDraw(Canvas canvas) {
super.onDraw(canvas);
// 根据Matrix绘制一个变换后的图片
canvas.drawBitmap(mBitmap, mPolyMatrix, null);
}
}文章发出后有小伙伴在GitHub上提出疑问,说此处讲解到并不清楚,尤其是最后的一个参数,所以特此补充一下内容。
我们知道pointCount支持点的个数为0到4个,四个一般指图形的四个角,属于最常用的一种情形,但前面几种是什么情况呢?
发布此文的时候之所以没有讲解0到3的情况,是因为前面的几种情况在实际开发中很少会出现,
才不是因为偷懒呢,哼。
| pointCount | 摘要 |
|---|---|
| 0 | 相当于reset |
| 1 | 相当于translate |
| 2 | 可以进行 缩放、旋转、平移 变换 |
| 3 | 可以进行 缩放、旋转、平移、错切 变换 |
| 4 | 可以进行 缩放、旋转、平移、错切以及任何形变 |
从上表我们可以观察出一个规律, 随着
pointCount数值增大setPolyToPoly的可以操作性也越来越强,这不是废话么,可调整点数多了能干的事情自然也多了。只列一个表格就算交代完毕了显得诚意不足,为了彰显诚意,接下来详细的讲解一下。
为什么说前面几种情况在实际开发中很少出现?
作为开发人员,写出来的代码出了要让机器"看懂",没有歧义之外,最重要的还是让人看懂,以方便后期的维护修改,从上边的表格中可以看出,前面的几种种情况都可以有更直观的替代方法,只有四个参数的情况下的特殊形变是没有替代方法的。
测控点选取位置?
测控点可以选择任何你认为方便的位置,只要src与dst一一对应即可。不过为了方便,通常会选择一些特殊的点: 图形的四个角,边线的中心点以及图形的中心点等。不过有一点需要注意,测控点选取都应当是不重复的(src与dst均是如此),如果选取了重复的点会直接导致测量失效,这也意味着,你不允许将一个方形(四个点)映射为三角形(四个点,但其中两个位置重叠),但可以接近于三角形。。
作用范围?
作用范围当然是设置了Matrix的全部区域,如果你将这个Matrix赋值给了Canvas,它的作用范围就是整个画布,如果你赋值给了Bitmap,它的作用范围就是整张图片。
接下来用示例演示一下,所有示例的src均为图片大小,dst根据手势变化。
pointCount为0
pointCount为0和reset是等价的,而不是保持matrix不变,在最底层的实现中可以看到这样的代码:
if (0 == count) {
this->reset();
return true;
}pointCount为1
pointCount为0和translate是等价的,在最底层的实现中可以看到这样的代码:
if (1 == count) {
this->setTranslate(dst[0].fX - src[0].fX, dst[0].fY - src[0].fY);
return true;
}平移的距离是dst - src.
当测控点为1的时候,由于你只有一个点可以控制,所以你只能拖拽着它在2D平面上滑动。
pointCount为2
当pointCount为2的时候,可以做缩放、平移和旋转。
pointCount为3
当pointCount为3的时候,可以做缩放、平移、旋转和错切。
pointCount为4
当pointCount为4的时候,你可以将图像拉伸为任意四边形。
上面已经用图例比较详细的展示了不同操控点个数的情况,如果你依旧存在疑问,可以获取代码自己试一下。
boolean setRectToRect (RectF src, // 源区域
RectF dst, // 目标区域
Matrix.ScaleToFit stf) // 缩放适配模式简单来说就是将源矩形的内容填充到目标矩形中,然而在大多数的情况下,源矩形和目标矩形的长宽比是不一致的,到底该如何填充呢,这个填充的模式就由第三个参数 stf 来确定。
ScaleToFit 是一个枚举类型,共包含了四种模式:
| 模式 | 摘要 |
|---|---|
| CENTER | 居中,对src等比例缩放,将其居中放置在dst中。 |
| START | 顶部,对src等比例缩放,将其放置在dst的左上角。 |
| END | 底部,对src等比例缩放,将其放置在dst的右下角。 |
| FILL | 充满,拉伸src的宽和高,使其完全填充满dst。 |
下面我们看一下不同宽高比的src与dst在不同模式下是怎样的。
假设灰色部分是dst,橙色部分是src,由于是测试不同宽高比,示例中让dst保持不变,看两种宽高比的src在不同模式下填充的位置。
| src(原始状态) |  |
|---|---|
| CENTER |  |
| START |  |
| END |  |
| FILL |  |
下面用代码演示一下居中的示例:
public class MatrixSetRectToRectTest extends View {
private static final String TAG = "MatrixSetRectToRectTest";
private int mViewWidth, mViewHeight;
private Bitmap mBitmap; // 要绘制的图片
private Matrix mRectMatrix; // 测试etRectToRect用的Matrix
public MatrixSetRectToRectTest(Context context) {
super(context);
mBitmap = BitmapFactory.decodeResource(getResources(), R.drawable.rect_test);
mRectMatrix = new Matrix();
}
@Override
protected void onSizeChanged(int w, int h, int oldw, int oldh) {
super.onSizeChanged(w, h, oldw, oldh);
mViewWidth = w;
mViewHeight = h;
}
@Override
protected void onDraw(Canvas canvas) {
super.onDraw(canvas);
RectF src= new RectF(0, 0, mBitmap.getWidth(), mBitmap.getHeight() );
RectF dst = new RectF(0, 0, mViewWidth, mViewHeight );
// 核心要点
mRectMatrix.setRectToRect(src,dst, Matrix.ScaleToFit.CENTER);
// 根据Matrix绘制一个变换后的图片
canvas.drawBitmap(mBitmap, mRectMatrix, new Paint());
}
}判断矩形经过变换后是否仍为矩形,假如Matrix进行了平移、缩放则画布仅仅是位置和大小改变,矩形变换后仍然为矩形,但Matrix进行了非90度倍数的旋转或者错切,则矩形变换后就不再是矩形了,这个很好理解,不过多赘述,顺便说一下,前面的mapRect方法的返回值就是根据rectStaysRect来判断的。
设置sinCos值,这个是控制Matrix旋转的,由于Matrix已经封装好了Rotate方法,所以这个并不常用,在此仅作概述。
// 方法一
void setSinCos (float sinValue, // 旋转角度的sin值
float cosValue) // 旋转角度的cos值
// 方法二
void setSinCos (float sinValue, // 旋转角度的sin值
float cosValue, // 旋转角度的cos值
float px, // 中心位置x坐标
float py) // 中心位置y坐标简单测试:
Matrix matrix = new Matrix();
// 旋转90度
// sin90=1
// cos90=0
matrix.setSinCos(1f, 0f);
Log.i(TAG, "setSinCos:"+matrix.toShortString());
// 重置
matrix.reset();
// 旋转90度
matrix.setRotate(90);
Log.i(TAG, "setRotate:"+matrix.toShortString());结果:
setSinCos:[0.0, -1.0, 0.0][1.0, 0.0, 0.0][0.0, 0.0, 1.0]
setRotate:[0.0, -1.0, 0.0][1.0, 0.0, 0.0][0.0, 0.0, 1.0]矩阵相关的函数就属于哪一种非常靠近底层的东西了,大部分开发者很少直接接触这些东西,想要弄明白这个可以回去请教你们的线性代数老师,这里也仅作概述。
| 方法 | 摘要 |
|---|---|
| invert | 求矩阵的逆矩阵 |
| isAffine | 判断当前矩阵是否为仿射矩阵,API21(5.0)才添加的方法。 |
| isIdentity | 判断当前矩阵是否为单位矩阵。 |
求矩阵的逆矩阵,简而言之就是计算与之前相反的矩阵,如果之前是平移200px,则求的矩阵为反向平移200px,如果之前是缩小到0.5f,则结果是放大到2倍。
boolean invert (Matrix inverse)简单测试:
Matrix matrix = new Matrix();
Matrix invert = new Matrix();
matrix.setTranslate(200,500);
Log.e(TAG, "before - matrix "+matrix.toShortString() );
Boolean result = matrix.invert(invert);
Log.e(TAG, "after - result "+result );
Log.e(TAG, "after - matrix "+matrix.toShortString() );
Log.e(TAG, "after - invert "+invert.toShortString() );结果:
before - matrix [1.0, 0.0, 200.0][0.0, 1.0, 500.0][0.0, 0.0, 1.0]
after - result true
after - matrix [1.0, 0.0, 200.0][0.0, 1.0, 500.0][0.0, 0.0, 1.0]
after - invert [1.0, 0.0, -200.0][0.0, 1.0, -500.0][0.0, 0.0, 1.0]判断矩阵是否是仿射矩阵, 貌似并没有太大卵用,因为你无论如何操作结果始终都为true。
这是为什么呢?因为迄今为止我们使用的所有变换都是仿射变换,那变换出来的矩阵自然是仿射矩阵喽。
判断是否是仿射矩阵最重要的一点就是,直线是否仍为直线,简单想一下就知道,不论平移,旋转,错切,缩放,直线变换后最终仍为直线,要想让isAffine的结果变为false,除非你能把直线掰弯,我目前还没有找到能够掰弯的方法,所以我仍是直男(就算找到了,我依旧是直男)。
简单测试:
Matrix matrix = new Matrix();
Log.i(TAG,"isAffine="+matrix.isAffine());
matrix.postTranslate(200,0);
matrix.postScale(0.5f, 1);
matrix.postSkew(0,1);
matrix.postRotate(56);
Log.i(TAG,"isAffine="+matrix.isAffine());结果:
isAffine=true
isAffine=true判断是否为单位矩阵,什么是单位矩阵呢,就是文章一开始的那个:
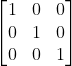
新创建的Matrix和重置后的Matrix都是单位矩阵,不过,只要随意操作一步,就不在是单位矩阵了。
简单测试:
Matrix matrix = new Matrix();
Log.i(TAG,"isIdentity="+matrix.isIdentity());
matrix.postTranslate(200,0);
Log.i(TAG,"isIdentity="+matrix.isIdentity());结果:
isIdentity=true
isIdentity=false通过前面的代码和示例,我们已经了解了Matrix大部分方法是如何使用的,这些基本的原理和方法通过组合可能会创造出神奇的东西,网上有很多教程讲Bitmap利用Matrix变换来制作镜像倒影等,这都属于Matrix的基本应用,我就不在赘述了,下面我简要介绍几种然并卵的小技巧,更多的大家可以开启自己的脑洞来发挥。
在之前的文章Matrix原理中我们提到过Matrix最根本的作用就是坐标映射,将View的相对坐标映射为屏幕的绝对坐标,也提到过我们在onDraw函数的canvas中获取到到Matrix并不是单位矩阵,结合这两点,聪明的你肯定想到了我们可以从canvas的Matrix入手取得View在屏幕上的绝对位置。
不过,这也仅仅是一个然并卵的小技巧而已,使用getLocationOnScreen同样可以获取View在屏幕的位置,但如果你是想让下一任接盘侠弄不明白你在做什么或者是被同事打死的话,尽管这么做。
简单示例:
@Override
protected void onDraw(Canvas canvas) {
float[] values = new float[9];
int[] location1 = new int[2];
Matrix matrix = canvas.getMatrix();
matrix.getValues(values);
location1[0] = (int) values[2];
location1[1] = (int) values[5];
Log.i(TAG, "location1 = " + Arrays.toString(location1));
int[] location2 = new int[2];
this.getLocationOnScreen(location2);
Log.i(TAG, "location2 = " + Arrays.toString(location2));
}结果:
location1 = [0, 243]
location2 = [0, 243]这个全凭大家想象力啦,不过我搜了一下还真搜到了好东西,之前鸿洋大大发过一篇博文详细讲解了利用setPolyToPoly制造的折叠效果布局,大家直接到他的博客去看吧,我就不写了。
图片引用自鸿洋大大的博客,稍作了一下处理。
博文链接:
Android FoldingLayout 折叠布局 原理及实现(一)
Android FoldingLayout 折叠布局 原理及实现(二)
本篇基本讲解了Matrix相关的所有方法,应该是目前对Matrix讲解最全面的一篇中文文章了,建议配合上一篇Matrix原理食用效果更佳。
由于本人水平有限,可能出于误解或者笔误难免出错,如果发现有问题或者对文中内容存在疑问欢迎在下面评论区告诉我,请对问题描述尽量详细,以帮助我可以快速找到问题根源。
作者微博: @GcsSloop
Understanding Affine Transformations With Matrix Mathematics










